✨

3️⃣ 모터(전동기) 고정자 및 회전자의 유도 기전력

본 글은 이전 글과 이어집니다.

Intro.

이전 글에서 모터 유도 전동기의 고정자 전압 방정식과 등가 회로를 유도하였다. 이 과정에서 모터(전동기) 고정자에 입력되는 전류 신호가 회전자에 전달되는 원리와 방향 및 크기를 유추할 수 있었다.

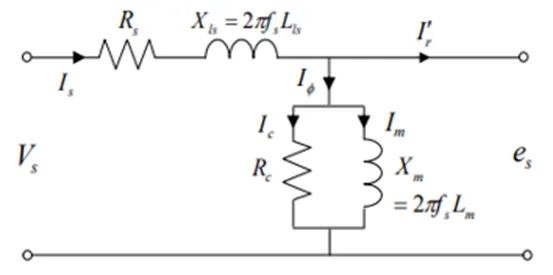
본 챕터에서는 이전 글에서 아직 규명하지 못한 그림 1의 유도 기전력(e_s)을 구해볼 것이다. 그리고 이를 이용해 다음 챕터에서 모터 회전자의 등가 회로를 유도하고, 이를 모터 고정자 측과 결부시켜 모터 전체의 등가회로를 유도해 볼 것이다. 이를 통해, 우리는 다음 챕터에서 다룰 유도 전동기의 여러 특성들에 대해 이해할 수 있다.

그림 1. 고정자 권선의 등가 회로

해당 챕터에서 모든 대문자 수학 기호(예:

V_s

)는 실효값(RMS) 혹은 고정된 상수 값을 의미하고, 모든 소문자 수학 기호(예:

v_s

)는 시간에 따라 변화할 수 있는 변수를 의미한다.

모터(전동기) 고정자 및 회전자의 유도 기전력

1) 고정자의 유도 기전력

그림 1의 등가 회로를 해석하기 위해서는 아직 정의되지 않은 유도 기전력을 정의 해야 할 필요가 있다. 유도 기전력의 정의를 위해, 유도 기전력이 권선에 쇄교 자속(λ_s)의 시간당 변화율이라는 점을 상기해야 한다. 결과적으로 우리는 이번 절에서 공극 자속(∅)을 정의해야 한다.

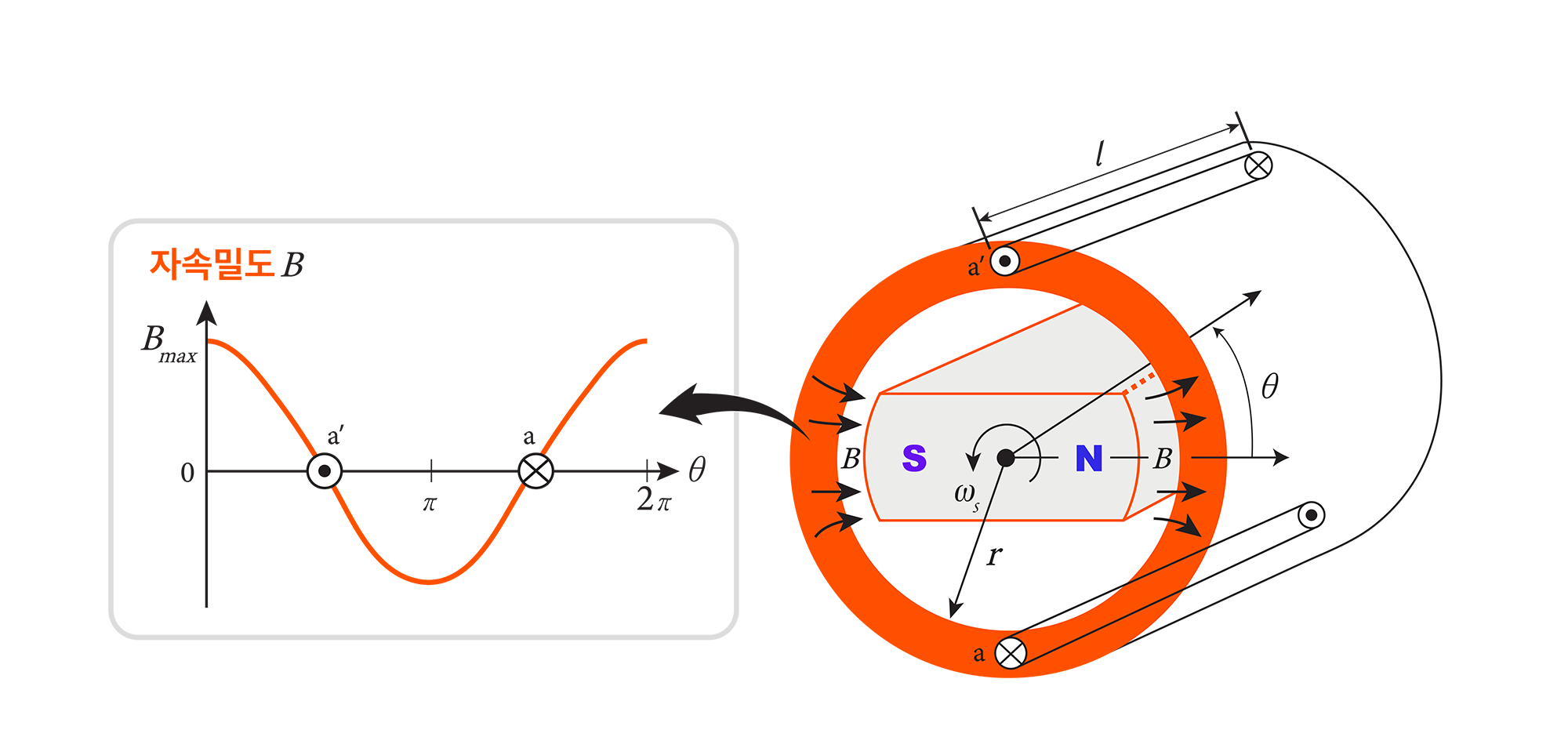
이를 보다 쉽게 이해하기 위해 그림 2와 같이, 회전 자계가 a상 권선 축(θ=0°)에 위치하고, 서서히 회전하고 있는 상태를 가정하자. 회전 자계가 회전함에 따라 자속 밀도는 그림 2의 도표와 같이 정현파 형태로 형성되며, 공극 자속 밀도(B)는 식(1)과 같이 회전 자계의 회전각(θ)의 함수로 표현될 수 있다.

그림 2. 회전 자계와 공극 자속 밀도

B(θ)=B_{max}cosθ

[T]

(1)

이 때,

B_{max}

는 자속 밀도의 최댓값이다.

위의 공극 자속 밀도를 활용해 공극 자속을 표현하면, 식 (2)와 같이 공극 자속 밀도와 회전 자계의 회전각에 따른 함수로 나타낼 수 있다.

∅=\int_{-{2 \over π}}^{2 \over π}B(θ)lrdθ=2B_{max}lr

[Wb]

(2)

이 때,

l

은 고정자 축의 길이[m],

r

은 공극의 평균 반지름[m]이다.

이제 a상의 권선에 쇄교 하는 자속의 양을 계산해보자. 고정자 유효 권선 수를

N_s

라 할 때, 회전 자계의 위치가

θ=0°

의 경우 a상 권선의 쇄교 자속은 최대

(N_s∅), θ=90°

에서는 0,

θ=180°

에서는 반대 방향으로 최대

(-N_s∅), θ=270°

에서는 다시 0이 된다.

그러므로, 시간에 따른 a상 권선의 쇄교 자속(

λ_a

)은 식 (3)과 같이 표현되고, 결과적으로 a상의 유도 기전력

(e_a)

은 식 (4)와 같이 표현된다.

(공극 자속은 시간에 대한 함수가 아니기 때문에, 편의상

∅

로 표현한다.)

λ_a=N_s∅cosθ=N_s∅cos w_st

(3)

e_a={-dλ \over dt} = w_sN_s∅sinw_st = E_{max}sinw_st

(4)

이 때,

w_s

는 각속도,

t

는 시간,

E_{max}

는 최대 유도 기전력이다.

나머지 b, c상은 a상과 120º, 240º 의 위상차가 있으므로, 각각 식 (5)와 (6)으로 표현된다.

e_b=e_{max}sin(w_st-120°)

(5)

e_c=e_{max}sin(w_st-240°)

(6)

각 상의 유도 기전력의 실효값은 다음과 같다.

E_{rms} = {E_{max} \over \sqrt{2}} = {w_sN_s∅ \over \sqrt{2}} =4.44f_sN_s∅

(7)

위 식 (7)을 통해 공극 자속은 유도 기전력과 주파수의 비에 비례

(∅ ∝E/f)

함을 알 수 있고, 이 원리를 사용해 유도 전동기의 속도를 제어한다.

2) 회전자의 유도 기전력

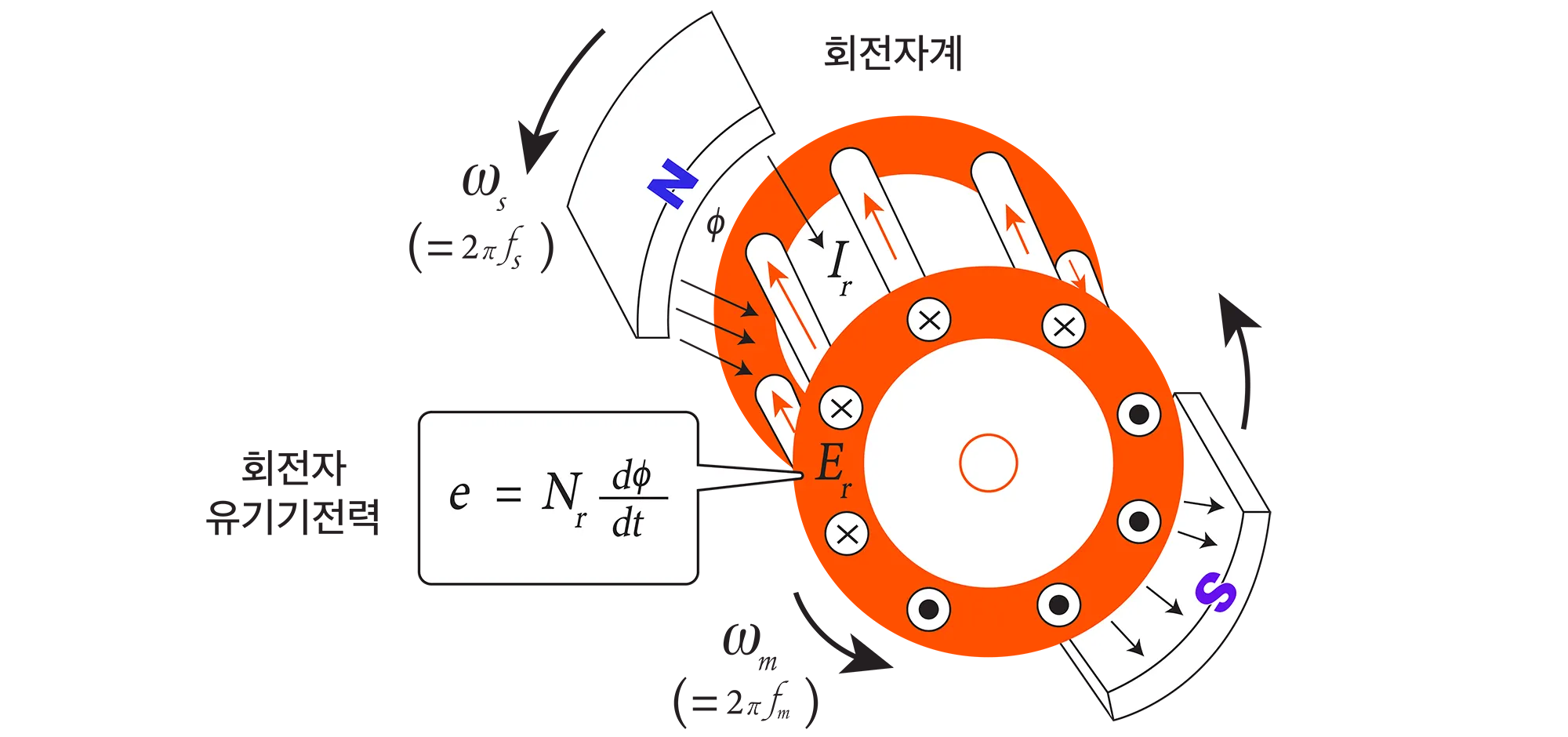
전동기 내 회전자 권선은 교류 전원에 직접 연결되어 있지 않고, 단락 되어 있기 때문에 우선 회전자 권선에 전류를 흐르게 하는 전원이 무엇인지 알아야 한다. 그림 3에서 관찰할 수 있듯이, 앞 절에서 살펴본 고정자 권선에 의해 공극에 발생된 회전 자계는 고장자 권선 뿐 아니라 회전하고 있는 회전자 권선에도 유도 기전력을 발생 시킨다. 이 유도 기전력이 바로 회전자 권선에 전류를 흐르게 하는 전원

(E_r)

이다.

그림 3. 회전자 도체의 유도 기전력

식 (8)과 같이 회전자 유효 권선 수를

N_r

이라고 할 때, 회전자의 유도 기전력

(E_r)

은 고정자 권선의 유도 기전력과 동일하고, 단지 동작 주파수 및 유효 권선 등의 차이가 있다. 여기서 주목해야 할 점은, 회전자는 고정자와 달리 회전자 자체가 회전하고 있으므로 유도 기전력 또한 회전자의 속도에 영향을 받는다는 것이다.

결과적으로, 회전자의 도체는 회전자와 함께 회전하고 있고, 이 상대 속도의 주파수로 자속이 변동한다. 이 상대 속도를 슬립 주파수

(f_{slip})

라고 하며, 식 (9)와 같이 표현할 수 있다.

E_r=4.44f_{slip}N_r∅

(8)

f_{slip}=f_s-f_r

(9)

이 때,

f_s

는 회전 자계의 회전 속도,

f_r

은 회전자의 회전 속도이다.

이제 회전자 도체의 동작 주파수(슬립 주파수)에 대해 조금 더 살펴보자. 이를 위해 회전자 도체의 유도 기전력은 자속의 시간에 따른 변동

(d∅/dt)

에 비례한다는 점을 상기하면, 유도 기전력의 주파수는 자속이 변동하는 슬립 주파수와 동일하다는 것을 알 수 있다.

결과적으로, 슬립 주파수는 회전자 도체의 동작 주파수가 된다. 이를 통해 우리는 회전자의 회전 속도와 유도 기전력의 크기가 반비례한다는 것을 알 수 있다.

유도 기전력의 크기는 자속의 변동 주파수에 비례하기 때문에, 회전자의 회전 속도가 커지면, 슬립 주파수가 작아져 유도 기전력이 줄어들게 된다. 반대로, 회전자의 회전 속도가 작아지면, 슬립 주파수가 커져 유도 기전력이 커진다.

Conclusion

이번 챕터에서는 전동기 내 고정자 및 회전자의 유도 기전력에 대해 살펴보았다.

이 과정에서 우리는 자속을 유도하였고, 이를 통해 모터의 유도 기전력을 유도할 수 있었다. 또한, 고정자 및 회전자 각각의 운동 특성을 고려하여 유도 기전력을 계산하였으며, 서로 다른 운동(정지, 회전)에 따른 슬립에 대해서도 이해하게 되었다.

슬립은 유도 전동기에서 가장 주요한 특징 중에 하나로, 다음 챕터에서 보다 깊이 다루어질 것이다. 결과적으로 우리는 모터 내부의 유도 기전력에 대해 알게 되었고, 회전 속도와 슬립 그리고 유도 기전력에 대한 관계 또한 알게 되었다. 다음 챕터에서는 슬립에 대한 몇 가지 성질과 회전자 등가회로를 유도하여 전체 모터 등가회로를 유도해 볼 것이다.