홈
🎯

시계열 데이터를 사용한 기계 설비 고장 진단 및 예측: (3) 시간-주파수 분석 방법을 이용한 진동 신호 분석

지난 2장에서는 주파수를 통해 진동 신호를 분석하는 방법인 Fourier Transform에 대해서 알아보았습니다. 이어서 이번 장에서는 시간-주파수 분석 방법인 Short-Time Fourier Transform과 Wavelet Transform에 대해 알아보겠습니다.
<진동 신호를 사용한 기계 설비 고장 진단 및 예측> 시리즈 전편 보러가기

Intro.

모두들 지난 포스트의 주제였던 Fourier Transform에 대해 기억하시나요?
Fourier Transform은 시간 영역의 복잡한 신호를 주파수 영역에서 볼 수 있다는 장점이 있지만, 시간에 따른 주파수 변화까지는 알 수 없다는 단점이 있었죠.
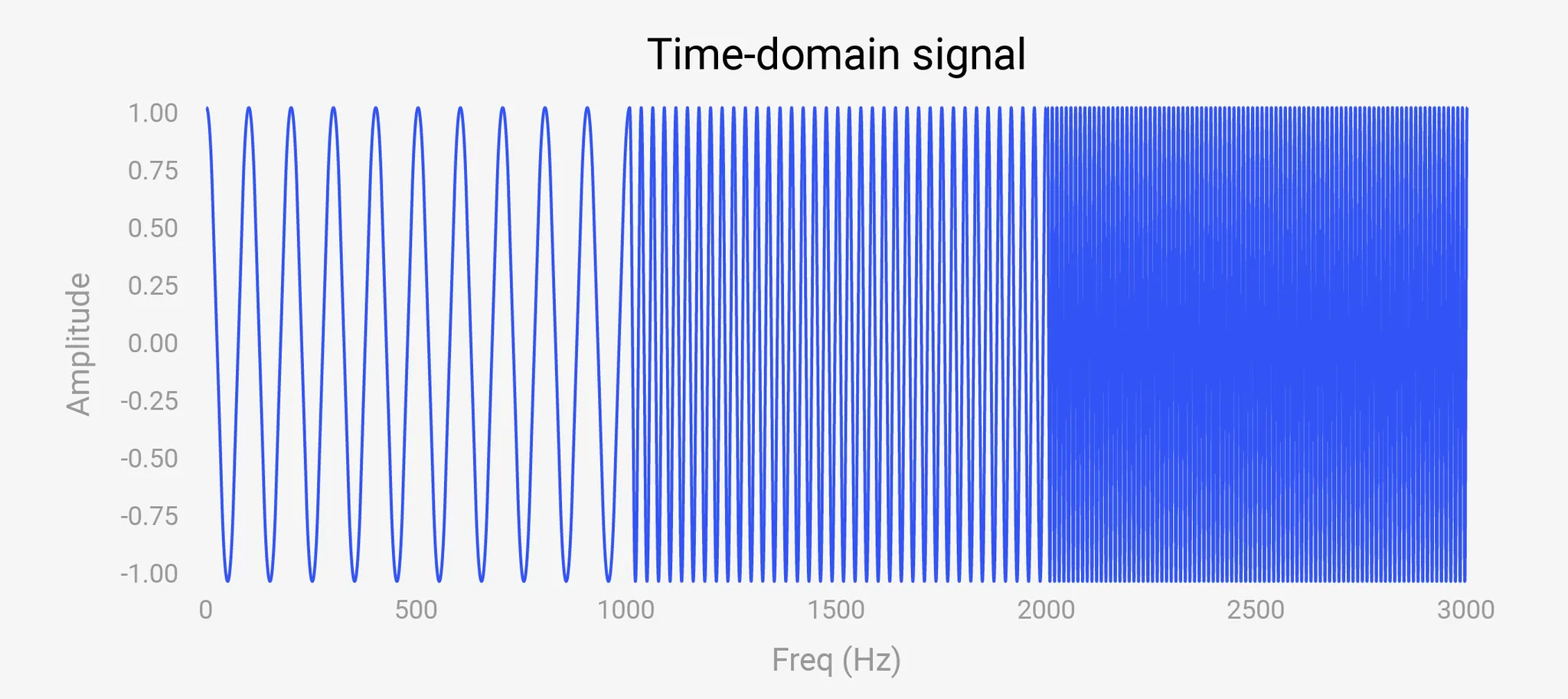
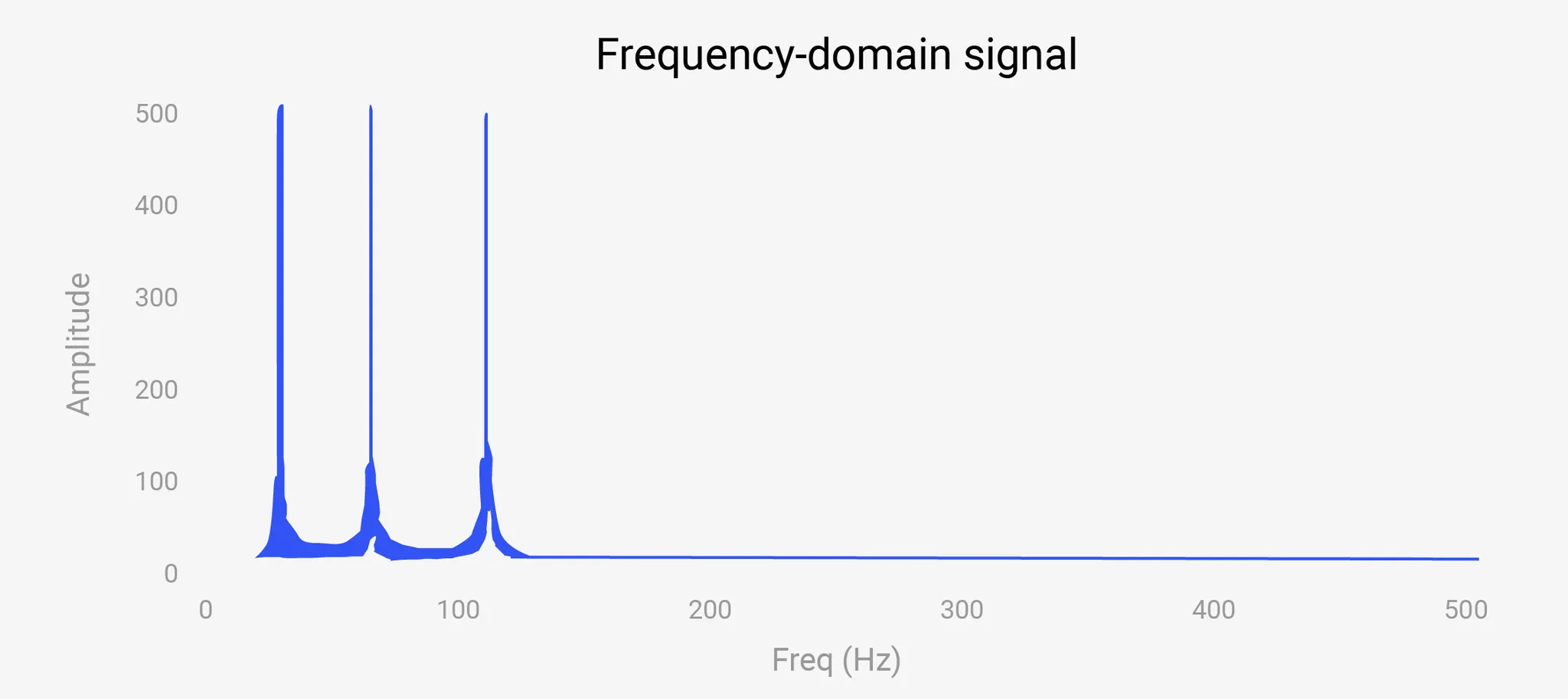
즉, 아래 그림처럼 일정한 주기가 아닌 시간의 흐름에 따라 주파수가 변화하는 신호라면, Fourier Transform으로는 각각의 주파수가 시간적으로 언제 존재하는지까진 알 수 없다는 한계가 있습니다.
그림 1. (위) 원 신호
(아래) 위의 원 신호를 Fourier Transform한 그래프
그렇다면 이렇게 시간에 따라 변화하는 신호를 짧은 시간 단위로 나눠서 본다면 어떤 주파수가 어떤 시간 구간에 있는지 알 수 있지 않을까요?

Short-Time Fourier Transform

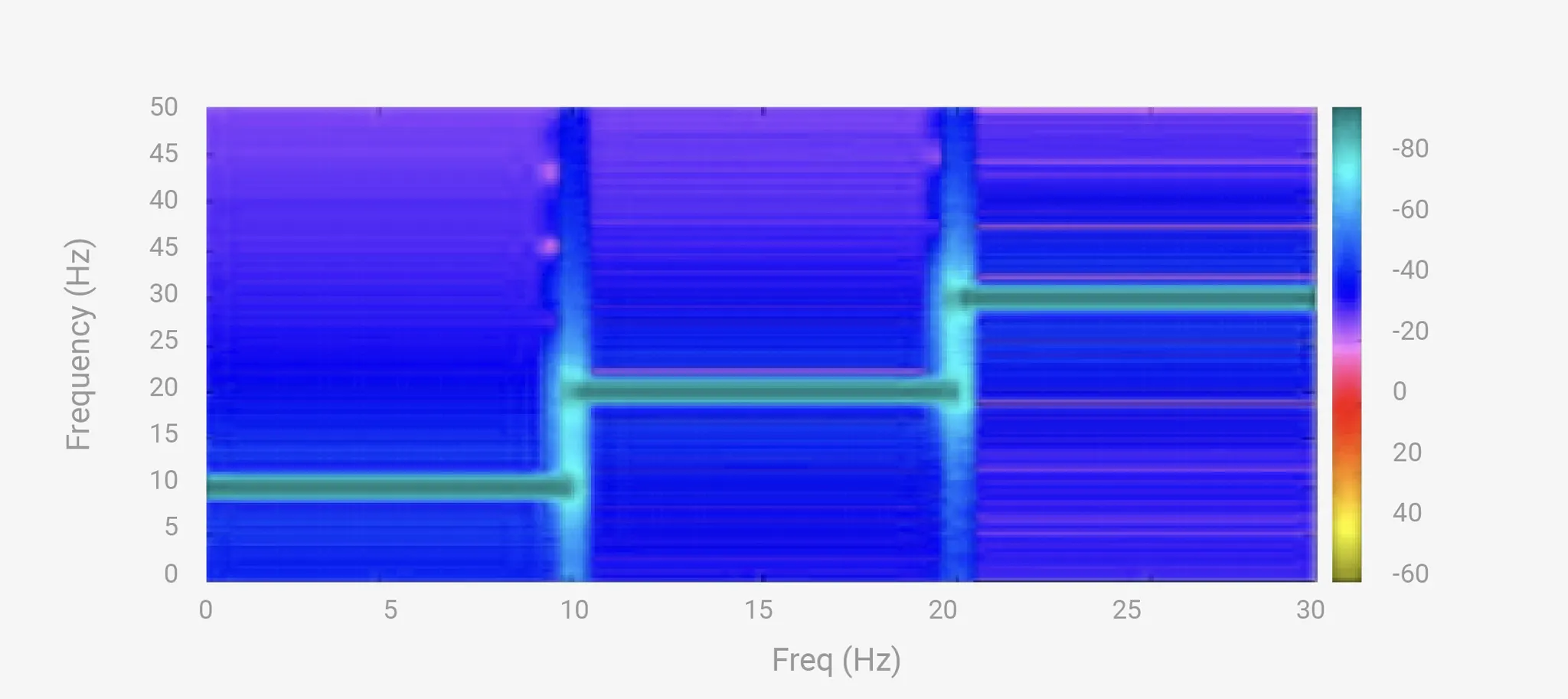
그래서 오늘 설명 드릴 첫번째 개념이 바로 Short-Time Fourier Transform (STFT)입니다. STFT에서는 일정한 시간 단위로 블록, 일명 Window를 나누는데, 각각 Window에 Fourier Transform을 적용합니다. 이를 통해 각 시간 구간마다 어떤 주파수들이 존재하는지 알 수 있죠.
그림 2. STFT를 통한 시간-주파수 그래프
여기서 Window의 너비가 10초라는 건 바로 눈에 들어오네요!
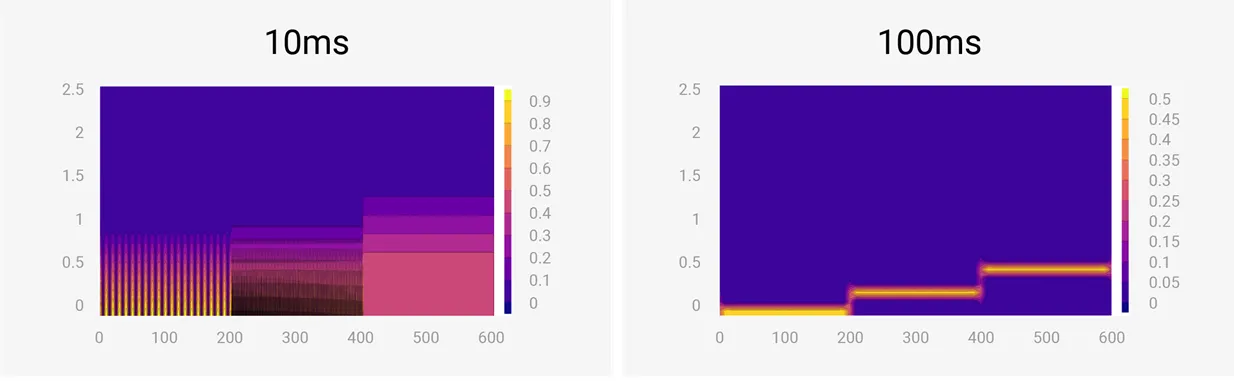
이러한 특징은 반대로 생각하면 단점으로도 작용할 수 있는데요. Window가 너무 좁으면 주파수 영역의 해상도가 떨어지고, 반대로 Window가 너무 넓으면, 시간 영역 해상도가 떨어집니다. 해상도가 떨어진다는 건 다른 말로 분해능이 떨어진다고도 표현하죠. (원프레딕트 윤병동 대표님의 이전 글 PHM 용어사전 참고)
그림 3. 왼쪽 10ms Window, 오른쪽 100ms Window
그래프 상단의 Window가 커질수록 주파수가 명확하게 보이시죠?
그렇다면 어떻게 해야 시간과 주파수, 두 가지 영역의 해상도를 모두 높일 수 있을까요? 주파수의 크기에 따라 Window 범위를 다르게 적용하면 가능합니다. [1]

Wavelet Transform

STFT에서는 고정된 Window 사이즈에 대해서만 계산할 수 있어서 시간 분해능과 주파수 분해능 중 하나를 포기해야만 했다면, Wavelet Transform은 Window 크기를 상황에 따라 바꿔가며 활용할 수 있습니다. 고주파는 Window를 더 잘게 쪼개서 시간 분해능을 높여서 보고, 반대로 저주파는 Window를 크게 적용해서 본다면, 시간과 주파수 해상도를 모두 놓치지 않을 수 있죠.
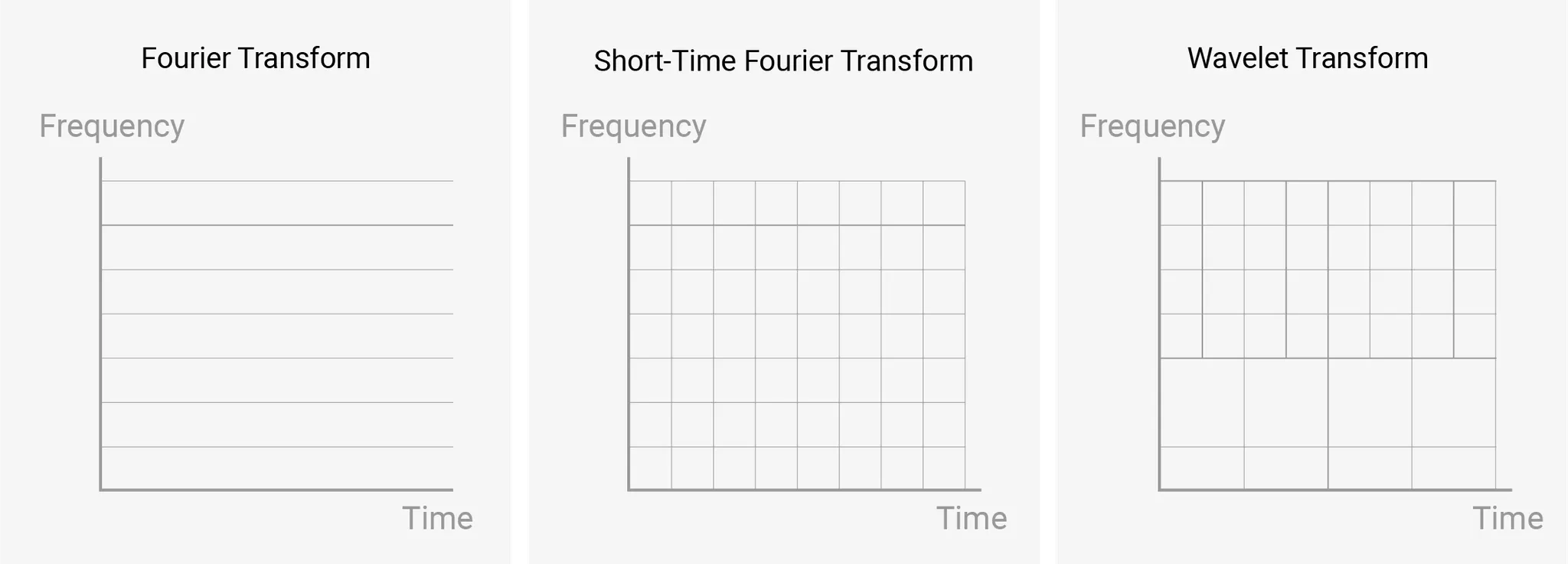
그렇다면 이쯤에서 Fourier Transform과 STFT, 그리고 방금 말씀드린 Wavelet Transform까지 한 번 비교해볼까요?
그림 4. Fourier Transform VS Short-Time Fourier Transform VS Wavelet Transform
이전 포스트에서 Fourier Transform은 다양한 주파수를 갖는 사인 곡선을 기본 함수로 사용하여, 시간 도메인에서의 신호를 주파수 도메인으로 변환한다고 했던 것 기억하시나요?
Wavelet Transform은 기존에 정의된 웨이블릿 함수를 기본 함수(모 웨이블릿, mother wavelet)로 사용하여 신호를 변환하는 방법이고, 아래와 같은 공식으로 나타날 수 있습니다.
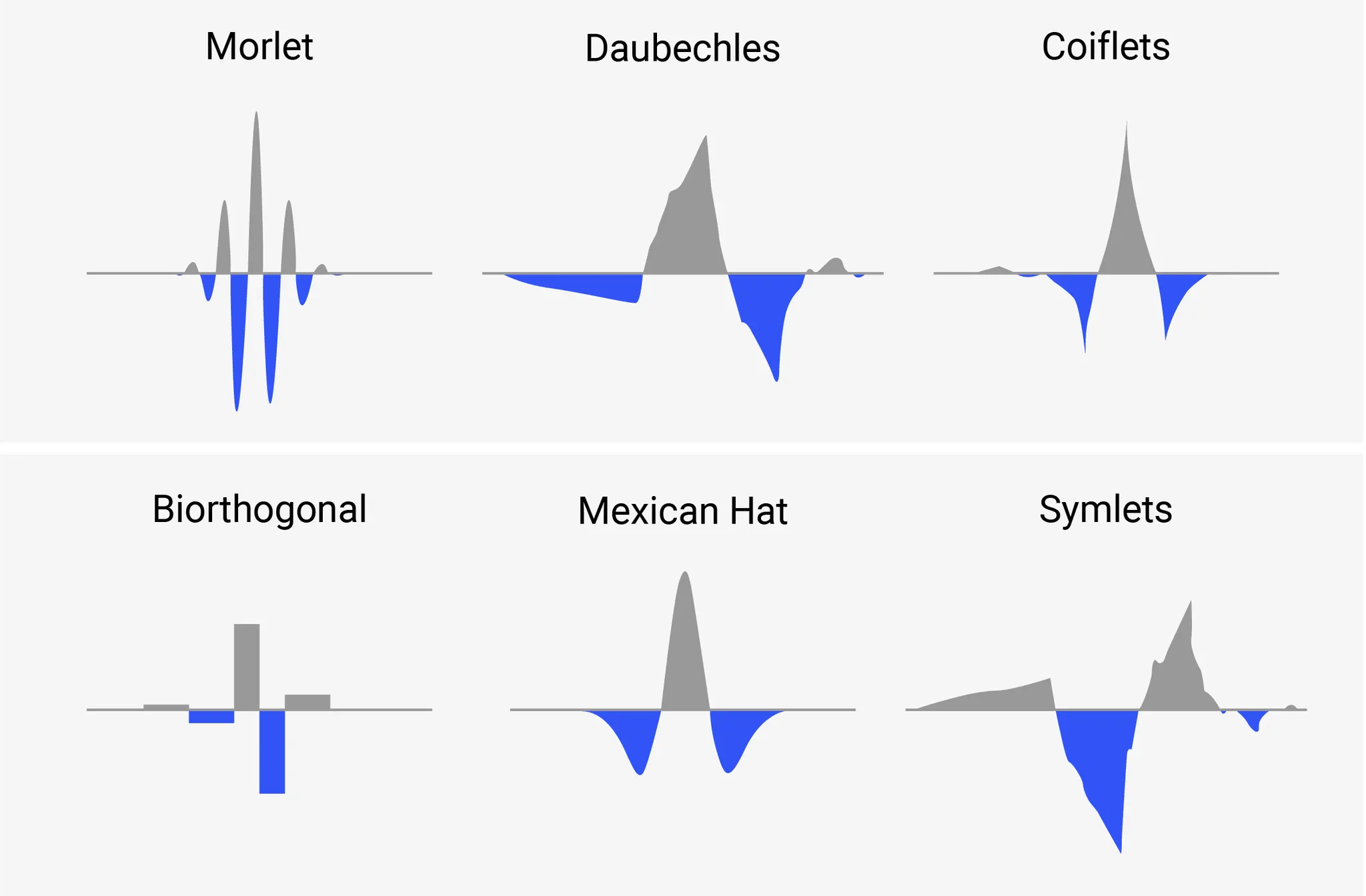
T(a,b)=1a∫−∞∞x(t)ψ∗(t−b)adtT(a,b)=\frac{1}{\sqrt a}\int_{-\infty}^{\infty}{x(t)\psi^\ast\frac{\left(t-b\right)}{a}d_t}
이 변환은 시간 영역에서의 신호를 웨이블릿 함수를 기준으로 합니다. 웨이블릿은 아래와 같이 다양한 종류로 나타나기 때문에, 필요에 따라 유연하게 하나를 선택해서 사용할 수 있죠. 웨이블릿 종류를 시간에 맞춰 Scaling(신호의 크기를 확장 또는 축소)하거나 Shifting(신호를 시간축 상의 특정 위치로 평행 이동)하여 복잡한 신호도 분석할 수 있습니다.
그림 5. 다양한 종류의 웨이블릿
Wavelet Transform은 분석의 목적에 따라서 Continuous Wavelet Transform (CWT)과 Discrete Wavelet Transform (DWT)으로 나눌 수 있습니다.
•
CWT은 매개변수를 매우 미세하게 이산화한 후 모 웨이블릿을 적용하는 방법으로, 시간 주파수 분석 및 시간적으로 국부화된 주파수 성분의 필터링 등 연속적인 스펙트럼 분석하는 데 쓰입니다.
•
DWT은 웨이블릿 변환 매개변수를 이산화하여 나타나는 것을 의미하는데, 신호 및 이미지의 노이즈 제거하거나 데이터를 압축하는 데 주로 사용되고 있습니다. [2]

Conclusion

총 3장에 걸쳐서 진동 신호 기초 용어부터, Fourier Transform, 그리고 STFT와 Wavelet Transform까지 진동 신호를 분석하기 위해 꼭 알아야 하는 필수 개념에 대해 소개하는 시간을 가졌습니다.
신호를 측정하고 분석하는 개념에 대해 알아보았으니, 이제는 실전에도 적용해야겠죠?
그래서 다음 장으로는 신호 분석을 넘어 실제로 고장을 진단하기 위해 사용되는 방법에 대한 내용을 준비했습니다! 원프레딕트가 그동안 실제 산업 환경에서 GuardiOne 솔루션을 통해 고장 진단을 하며 직접 경험한 방법들에 대해 소개하려고 하니 많은 기대 부탁드립니다.
신호 분석을 통한 기계 설비 진단 및 예측 시리즈 다음 편 보러가기
•
진동 신호를 사용한 기계 설비 고장 진단 및 예측: (3) 시간-주파수 분석 방법을 이용한 진동 신호 분석

참조

[1] Gröchenig, Foundations of Time-Frequency Analysis, Birkhäuser, Boston, 2001.
[2] Saribulut, Fundamentals and literature review of wavelet transform in power quality issues, 2013

이 글을 쓴 사람

나 대 엽 | 베타(β)팀
원프레딕트 베타팀에서 데이터 사이언티스트로서 일을 하고 있습니다.
어떤 일이든 가치 있는 일이라고 생각하며, 새로운 것을 배우거나 공부하는 것을 즐깁니다.
오 혜 원 | 마케팅팀
원프레딕트 마케팅팀에서 홍보와 대내외 커뮤니케이션을 담당하고 있습니다.
천상 문과생이지만 최첨단 초일류 AI 회사에 다니는만큼 어디 가서 창피 당하지 않을 정도의 이과적 소양을 쌓고자 노력하는 중입니다.
물욕이 강한 편이라, 하고 싶은 거, 입고 싶은 거, 먹고 싶은 거 다 사기 위해 오늘도(뚠뚠) 개미는(뚠뚠) 열심히(뚠뚠) 일하고 있습니다.
원프레딕트 홈페이지 https://onepredict.ai/
원프레딕트 블로그 https://blog.onepredict.ai/
원프레딕트 기술 블로그 https://tech.onepredict.ai