홈
⏳

시계열 데이터를 사용한 기계 설비 고장 진단 및 예측: (1) 진동 기초 용어

Intro.

여러분은 몸이 아파서 병원에 가신적이 있으신가요? 병원에 가면 보통 의사선생님께 진찰을 받으면서 증상의 종류에 따라 청진기 검사, 혈액검사 등 크고 작은 다양한 검사를 받게 됩니다. 여러분의 몸 상태에 대한 정량적인 정보가 있어야 정확한 진단을 내릴 수 있기 때문입니다.
주체와 방법만 변경될 뿐, 산업설비에 이상징후가 있을 때 설비를 진단하는 것도 마찬가지입니다.
예를 들어, 원프레딕트는 변압기, 모터, 터빈, 모빌리티 등 다양한 산업 설비의  진단 및 예측 솔루션을 제공합니다. 진단 대상에 따라 상이하지만 대부분의 경우, 진동 신호를 분석하고 도메인 ∙ AI 기반 알고리즘을 기반으로 상태 진단 및 예측을 수행합니다.
따라서 병원에 가서 진료를 받는 모습을 ‘진동 기반 산업설비 상태 진단’ 사례에 대입하면 진단 대상을 [사람→기계], 데이터를 [검사 수치→진동 측정값], 진단 주체를 [의사→진단 알고리즘]으로 생각해볼 수 있습니다.
한편, 의사의 환자 진단 방법이 다양한 것처럼, 진동 신호 기반의 기계 설비 진단 방법론도 다양하게 개발되어 왔습니다.
이번 기술 블로그 시리즈에서는 진동 신호를 사용한 기계 설비의 고장 진단 및 예측에 대해 알아보겠습니다. 특히, 이번 글에서는 데이터의 샘플링 주파수, 샘플링 주기, 샘플링 속도 등의 진동 분석의 기초용어를 알아보는 시간을 가지겠습니다.

진동 신호 분석 기초용어 및 개념

이번 장에서는 국제 표준인 ISO 내용을 기반으로 앞서 언급한 진동 신호 분석 기초용어와 개념에 대해서 이야기하겠습니다.
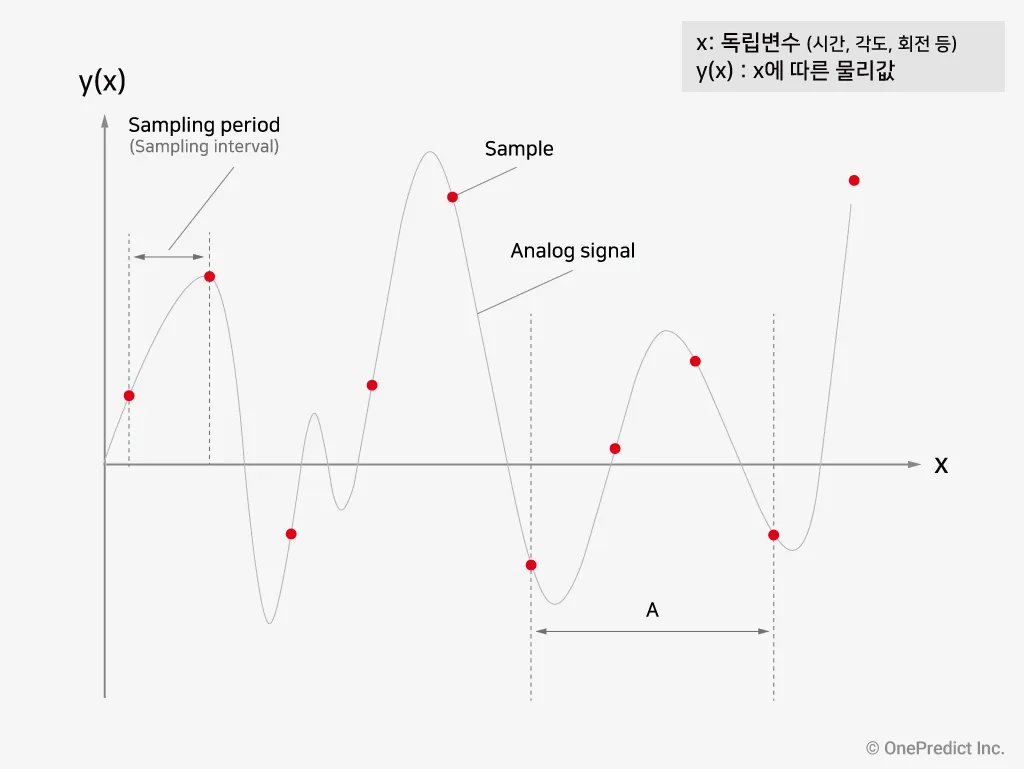
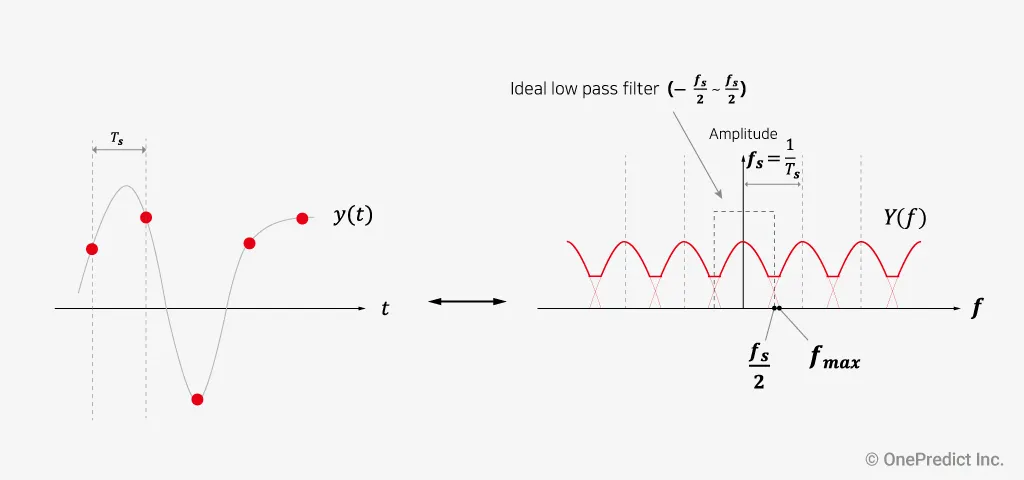
그림 1. 아날로그 신호의 샘플링 및 진동 기초 용어
1.
샘플링 (sampling)
Measurement of a varying physical quantity at a sequence of values of time, angle, revolutions or other mechanical, independent variable [1]
샘플링은 ‘시간, 각도, 회전 또는 기타 기계적 독립 변수의 연속값에서 변화하는 물리적 양의 측정’을 의미합니다.
그림 1을 참고하면, 독립변수(x)에 따라 변화하는 물리값 y(x)를 샘플링하는 모습을 볼 수 있습니다. 이처럼 독립 변수의 연속값에 따른 아날로그 신호를 측정하는 행위를 ‘샘플링한다.’ 라고 말할 수 있습니다.
2.
샘플링 주기 (sampling period)
Duration of time between two successive samples [1]
샘플링 주기는 ‘두 개의 연속 샘플들 사이의 지속시간’을 의미합니다. 그림 1을 참고하면, 독립변수(x)가 시간일때 두 연속적인 빨간점 사이의 간격을 샘플링 주기라고 할 수 있습니다. 예를 들어, 진동 신호의 샘플링 주기가 0.1초이면 샘플들 사이의 시간 간격이 0.1초란 뜻입니다.
3.
샘플링 주파수 (sampling frequency)
Number of samples per unit of time for uniformly sampled data [1]
샘플링 주파수는 ‘균일하게 샘플링된 데이터에 대한 시간 단위당 샘플 수’를 의미합니다. 예를 들어, 그림 1이 시간영역에서 균일하게 샘플링된 결과라고 가정하고 A가 2초라면, 해당 구간의 샘플 수는 4개이므로 샘플링 주파수는 2Hz (= 4 samples / 2 seconds)입니다. 이는 “초당 2개의 샘플 수를 얻는다.” 로 해석할 수 있습니다. 한편, 샘플링 주파수는 샘플링 주기와 역수 관계입니다.
따라서,
sampling  frequency=1sampling  periodsampling\;frequency = \frac{1}{sampling\;period}
이고, 만약 샘플링 주파수가 2Hz이면, 샘플링 주기는 0.5초입니다.
4.
샘플링 간격 (sampling interval)
Number of units (e.g. time, angle, revolutions) between two successive samples [1]
샘플링 간격은 그림 1과 같이 ‘두 개의 연속된 샘플 사이의 단위 수(예: 시간, 각도, 회전)’를 의미합니다. 일반적으로, 샘플링 간격은 시간영역에서 ‘샘플링 주기’와 비슷한 용어로 사용됩니다. 차이가 있다면, 샘플링 간격은 ‘샘플링 주기’의 시간(time) 단위에 덧붙여 각도, 회전 단위가 추가된 넓은 개념입니다.
5.
샘플링 속도 (sampling rate)
Number of samples per unit of time, angle, revolutions or other mechanical, independent variable for uniformly sampled data [1]
샘플링 속도는 ‘균일하게 샘플링된 데이터에 대한 시간, 각도, 회전 또는 기타 기계적 독립 변수당 샘플 수’를 의미합니다. 일반적으로, 샘플링 속도는 시간영역에서 ‘샘플링 주파수’와 비슷한 용어로 사용됩니다. 차이가 있다면, 샘플링 속도는 ‘샘플링 주파수’의 시간(time) 단위에 덧붙여 각도, 회전 단위가 추가된 넓은 개념입니다. 그리고 ‘샘플링 주파수’와 ‘샘플링 주기’의 관계처럼 ‘샘플링 속도’도 ‘샘플링 간격’과 역수 관계입니다.

나이퀴스트 주파수와 앨리어싱 현상

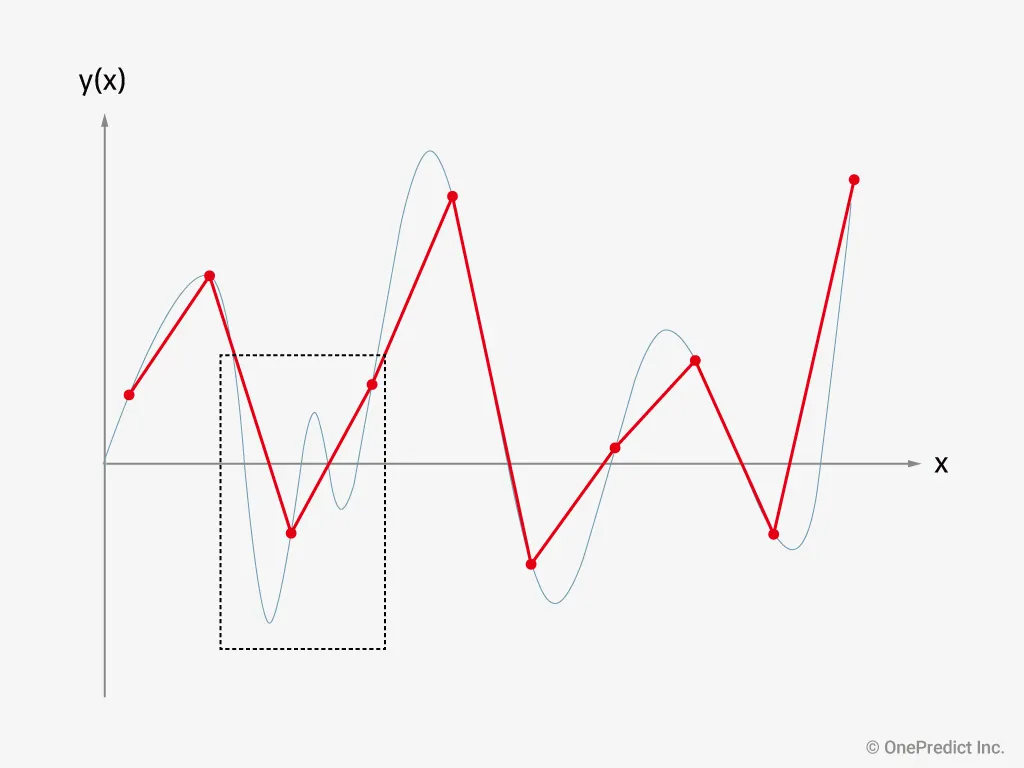
전 목차에서 그림 1을 통해 샘플링에 관한 기본적인 용어와 개념을 알아보았습니다. 혹시 그림 1을 보면서 이상한 부분을 보셨나요? 그림 1의 샘플들을 선으로 이어서 원래 아날로그 신호랑 비교해볼까요?
그림 2처럼 아날로그 신호의 일부 모습이 제대로 반영이 안된 것을 알 수 있습니다. 이처럼 샘플링 속도는 데이터의 모습을 제대로 반영하는데 있어서 매우 중요합니다. 이와 관련하여 나이퀴스트 주파수와 앨리어싱 현상에 대해 알아보겠습니다.
그림 2. 아날로그 신호(파랑)와 샘플링 신호(빨강) 비교
1.
나이퀴스트 주파수(Nyquist frequency)
Maximum usable frequency available in data taken at a given sampling rate [1]
나이퀴스트 주파수는 주어진 샘플링 속도로 수집한 데이터에서 사용 가능한 최대 주파수를 의미합니다. 이에 대한 수식은 다음과 같이 유도될 수 있습니다.
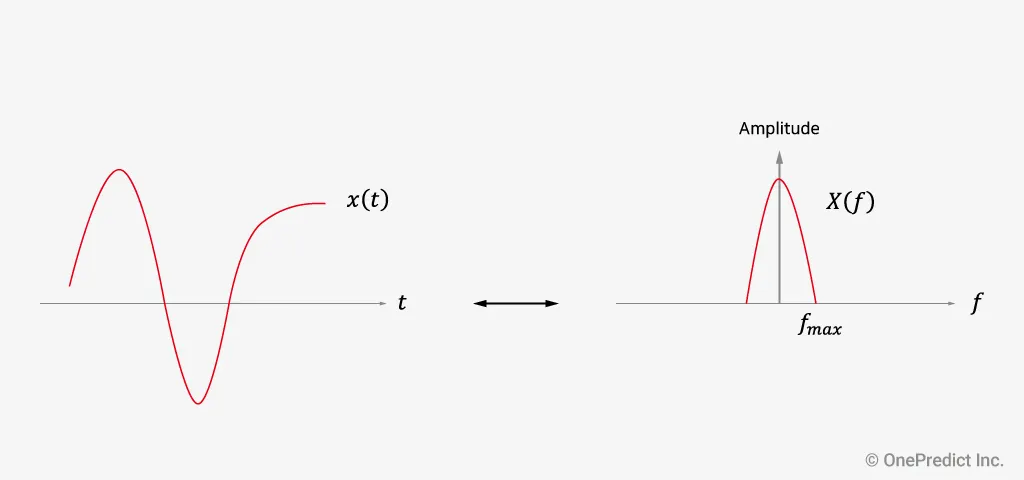
그림 3 원 신호와 주파수 스펙트럼
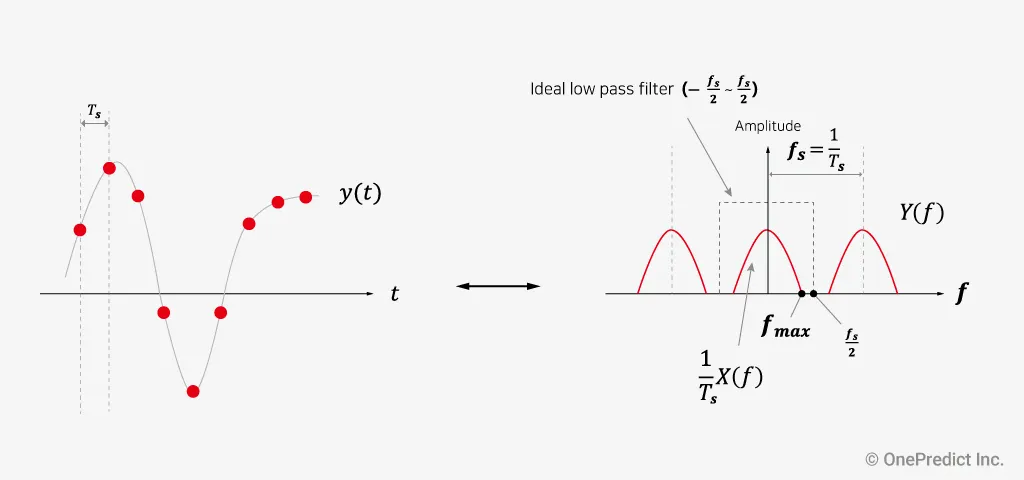
그림 4. 샘플링된 신호(fmax≤fs2f_{max} \leq \frac{f_s}{2})와 주파수 스펙트럼
그림 5. 샘플링된 신호(fmax>fs2f_{max} > \frac{f_s}{2} )와 주파수 스펙트럼
그림 3을 통해 원 신호 x(t)x(t)를 FFT한 X(f)X(f)를 볼 수 있습니다. 그리고 그림 4 왼쪽처럼, x(t)x(t)를 샘플링 주파수 fsf_s로 샘플링한 y(t)y(t)를 볼 수 있습니다. 한편, y(t)y(t)를 FFT한 Y(f)Y(f)는 Sampling theorem에 의해 X(f)X(f)와 다음과 같은 관계를 가집니다.
Y(f)=1Ts∑k→−∞∞X(f−kTs)Y(f) = \frac{1}{T_s}\sum_{k\to-\infty}^{\infty} X(f-\frac{k}{T_s})
즉 그림 4의 오른쪽처럼, Y(f)Y(f)는 샘플링 주파수 간격(fs=1Tsf_s=\frac{1}{T_s})마다 원 신호 스펙트럼 형상이 반복되어 나타납니다. 따라서fmax⁡≤fs2f_{\max} \leq \frac{f_s}{2} 이어야 low pass filter를 통한 원 신호 복원이 가능합니다. 만약 fmax⁡>fs2f_{\max} > \frac{f_s}{2} 이면, 그림 5과 같이 스펙트럼이 겹쳐서 신호가 왜곡되는 현상이 발생하기 때문에 원 신호로 복원할 수 없습니다. 결과적으로, 주어진 샘플링에서 사용가능한 최대 주파수가 존재하게 되고, 아래와 같은 수식으로 나이퀴스트 주파수(fNf_N )를 정리할 수 있습니다.
fN=fx2f_N = \frac{f_x}{2}
(fsf_s:sampling rate, fNf_N:Nyquist frequency)
예를 들어, 샘플링 속도(fsf_s)가 12,800Hz이라면 나이퀴스트 주파수(fNf_N)는 6,400Hz이고 최대로 측정 가능한 데이터의 범위가 6,400Hz이므로 수집한 데이터의 최대 주파수는 6,400Hz를 초과하지 않는 것이 좋습니다. 따라서 나이퀴스트 주파수를 고려하여 관심 주파수 범위를 벗어나지 않게 샘플링 속도를 설정해야 할 필요가 있습니다.
앨리어싱은 나이퀴스트 주파수 이상의 주파수 성분과 나이퀴스트 주파수 이하의 주파수성분의 혼합으로 인해서 스펙트럼 에너지가 잘못 표현된 것을 의미합니다. 즉 앨리어싱은 입력신호의 최대주파수가 나이퀴스트 주파수보다 작아서 측정된 신호를 정확히 표현하지 못하는 현상을 말합니다.
2.
앨리어싱(Aliasing)
False representation of spectral energy caused by mixing of spectral components above the Nyquist frequency with those spectral components below the Nyquist frequency [1]
앨리어싱은 나이퀴스트 주파수 이상의 주파수 성분과 나이퀴스트 주파수 이하의 주파수성분의 혼합으로 인해서 스펙트럼 에너지가 잘못 표현된 것을 의미합니다. 즉 앨리어싱은 입력신호의 최대주파수가 나이퀴스트 주파수보다 작아서 측정된 신호를 정확히 표현하지 못하는 현상을 말합니다.
3.
예시
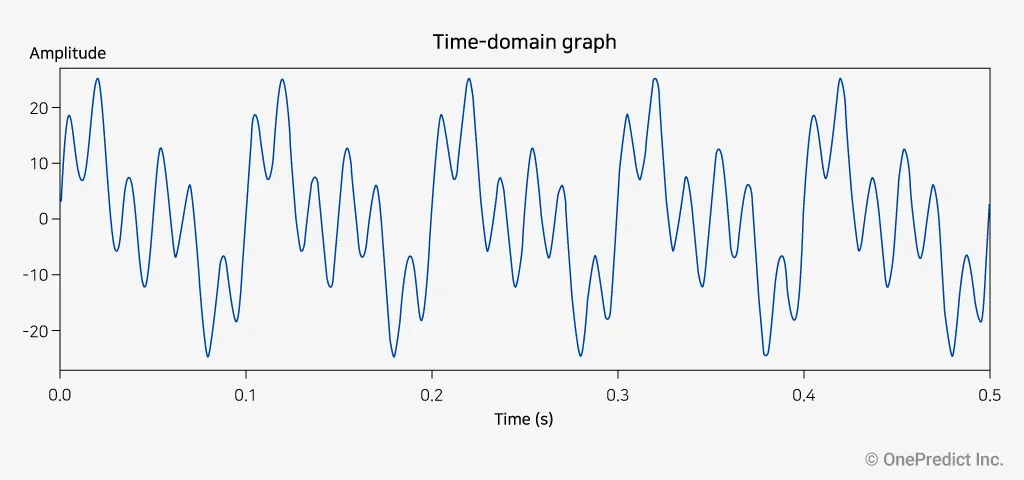
샘플링 주파수(fsf_s)가 20Hz, 40Hz, 1000Hz로 변화함에 따라 아래 주어진 수식의 그래프(그림6)가 어떻게 바뀌는지 Python을 활용하여 알아보겠습니다.
y(t)=10sin⁡(2π×f1×t)+10sin⁡(2π×f2×t)+10sin⁡(2π×f3×t)y(t)= 10\sin(2\pi\times f_1\times t)+10\sin(2\pi\times f_2 \times t)+10\sin(2\pi\times f_3 \times t)
(f1=10Hz,f2=20Hz,f3=60Hz)(f_1 = 10Hz, f_2 = 20Hz, f_3 = 60Hz)
그림 6. y(t)y(t)의 시간영역 그래프
1. 시간 영역

Conclusion

이번 글에서는 신호의 샘플링 주파수, 주기, 속도, 간격 등에 대한 개념을 알아보았으며, 샘플링된 신호의 나이퀴스트 주파수와 앨리어싱 현상의 예시와 해결 방법에 대해 알아보았습니다.
다음 글에서는 주파수 분석을 위해 사용되는  FFT(Fast Fourier transform) 알고리즘의 종류와 개념에 대해 알아보는 시간을 가질 예정입니다.
이 밖에도 원프레딕트 블로그에서는 산업 인공지능 관련 최신 기술에 대한 정보에 대한 다양한 주제의 글들이 주기적으로 업데이트되니 많은 관심 부탁드리겠습니다.
감사합니다.
<진동 신호를 사용한 기계 설비 고장 진단 및 예측> 시리즈 다음 편 보러가기
Reference [1] ISO 18431-1:2005 Mechanical vibration and shock — Signal processing — Part 1: General introduction
신호 분석을 통한 기계 설비 진단 및 예측
•
진동 신호를 사용한 기계 설비 고장 진단 및 예측: (1) 진동 기초 용어

이 글을 쓴 사람

김 강 휘 | 미래솔루션팀
새로운 것에 대해 호기심이 많고 시도해 보는 것을 좋아합니다.
원프레딕트의 미래를 책임질 산업설비의 솔루션 개발을 수행하고 있습니다. 여가 시간에는 맨몸운동, 블로그 작성, 재테크 공부 등을 하는 것을 좋아합니다.
원프레딕트 홈페이지 https://onepredict.ai/
원프레딕트 블로그 https://blog.onepredict.ai/
원프레딕트 기술 블로그 https://tech.onepredict.ai