홈
〰️

시계열 데이터를 사용한 기계 설비 고장 진단 및 예측: (2) 주파수 분석 방법을 이용한 진동 신호 분석

진동 신호는 기계 설비의 고장을 진단하고 예측하는 데에 필수적인 요소입니다. 지난 1편에서는 진동 신호에 대한 기초 용어들을 알아보았는데, 이번 2편에서는 샘플링된 진동 신호를 분석하는 방법 중 하나인 주파수 분석에 대해 심층적으로 정리해보려 합니다.
<진동 신호를 사용한 기계 설비 고장 진단 및 예측> 시리즈 전편 보러가기

Intro.

앞 장에서 한 차례 설명 드렸듯이, 원프레딕트는 산업 설비의 건전성을 진단하고 예측할 때 주로 진동 신호를 활용하기 때문에, 보다 정확하게 진동 신호를 분석하는 것은 끝나지 않는 원프레딕트의 숙제라고 할 수 있습니다.
진동 신호가 그림 1과 같이 간단하고 명확하게만 나타나준다면, 신호에 대한 정보를 얻기가 그렇게 어려운 일은 아니었을 텐데요.
그림 1. 우리가 원하는 단순하고 깔끔한 신호 그래프
실제 진동 신호는 노이즈 등의 이유로 굉장히 복잡한 형태를 띄고 있기 때문에, 우리가 구하고자 하는 특정 신호에 대한 정보를 얻기란 쉽지 않습니다.
그래서 이번 시간에는 이런 복잡한 신호를 단순한 신호의 형태로 바꿔서 볼 수 있는 방법에 대해 알아보려고 합니다.

Fourier Series

복잡한 신호를 단순한 신호로 바꾸기 위해서 가장 먼저 알아야 할 개념은 바로 Fourier Series입니다.
Fourier Series란 프랑스의 유명한 수학자이자 물리학자였던 Jean Baptiste Joseph Fourier (이하 푸리에) 가 열 방정식을 풀기 위해 처음 도입한 법칙입니다.
이 개념의 핵심부터 쉽게 말하면, 복잡한 신호는 다양한 주파수를 가진 신호들의 합이기 때문에 주기를 가지는 모든 신호는 아무리 복잡한 신호라도 단순한 신호로 표현이 가능하다는 것입니다.
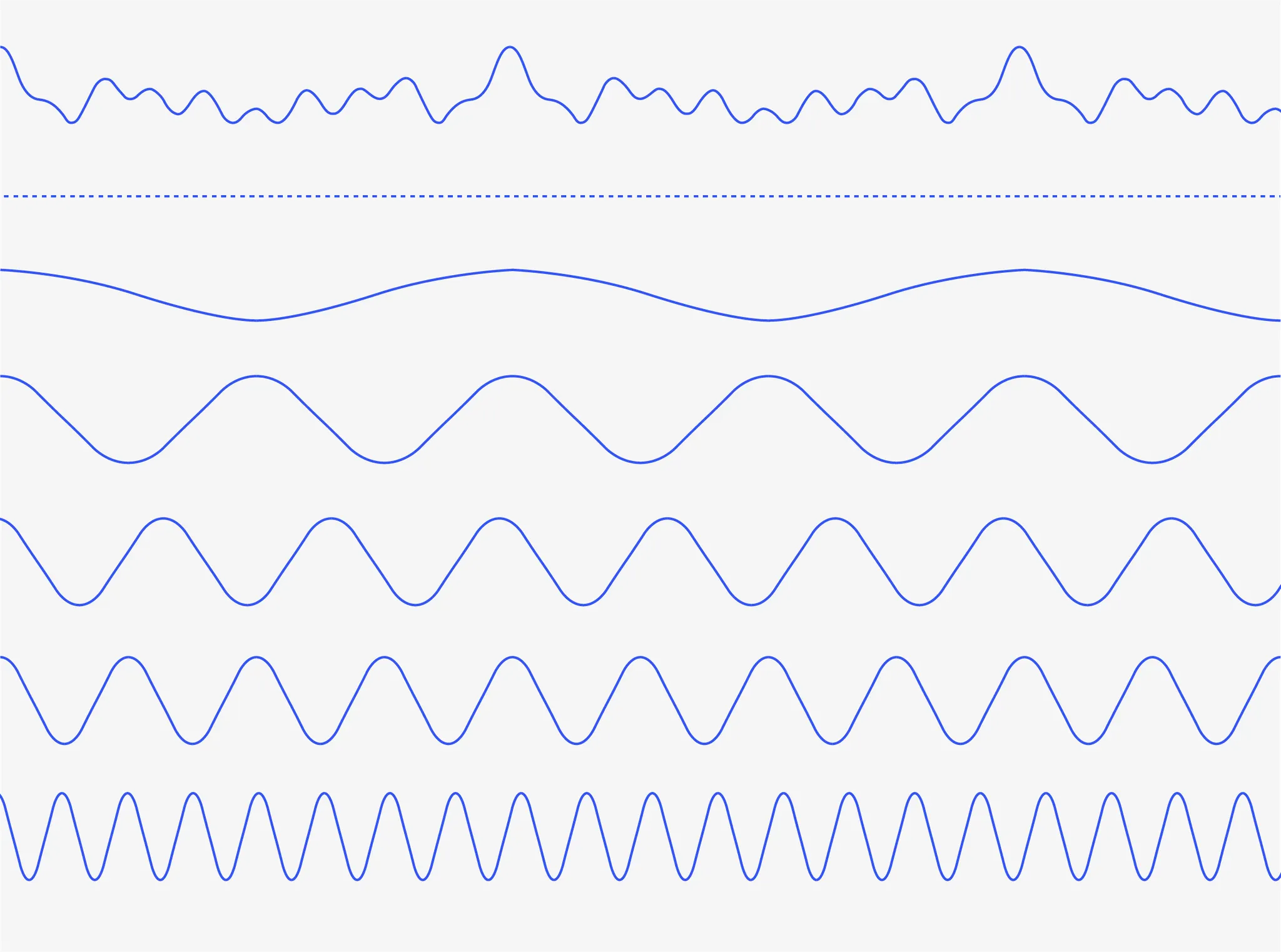
예를 들어 그림 2처럼 복잡한 그래프도 결국은 그 아래 그림 3의 여러 가지 그래프들이 합쳐져서 만들어진 것입니다.
그림 2. 여러 신호가 중첩된 복잡한 신호 그래프
그림 3. 분해된 개별 신호
Fourier Series에 따르면 우리가 현실에서 마주하는 복잡한 신호는 아래와 같이 삼각함수를 활용한 수식으로 나타내어, 간단한 신호로 분해할 수 있습니다.
x(t)=a02+∑n=0∞[ancos⁡(2πntTp)+bnsin⁡(2πntTp)]x(t)= {a_0 \over 2} + \sum^{\infty}_{n=0}[a_n \cos ({2\pi n t \over T_p}) + b_n \sin ({2\pi n t \over T_p})]
an=2Tp∫−Tp2Tp2x(t)cos⁡(2πntTp)dta_n = {2 \over T_p} \int^{T_p\over 2}_{- {T_p \over 2}} x(t) \cos ({ 2\pi n t \over T_p})dt
bn=2Tp∫−Tp2Tp2x(t)sin⁡(2πntTp)dtb_n = {2 \over T_p} \int^{T_p\over 2}_{- {T_p \over 2}} x(t) \sin ({ 2\pi n t \over T_p})dt
*x(t)x(t): 우리가 보는 복잡한 신호, TpT_p: 주기, an,bna_n, b_n: 각 주기에서의 신호의 계수(진폭)
삼각함수로 표현한 수식은 오일러 법칙에 의해 지수함수의 형태로 더 간단하게 표현할 수 있습니다. 바뀐 수식은 아래와 같습니다. (오일러 법칙에 대해 더 궁금하시다면 링크를 클릭해주세요!)
x(t)=∑−∞∞cnej2πnt/Tpx(t) = \sum^{\infty}_{-\infty} c_n e^{j2\pi n t / T_p}
cn=1Tp∫−Tp2Tp2x(t)e−j2πnt/Tpdtc_n = {{1} \over {T_p}} \int^{T_p \over 2}_{{-T_p \over 2}} x(t) e^{-j2\pi n t /T_p} dt
수식의 모양이 바뀌어 어려워 보이지만, 지수함수가 가장 간단한 신호(삼각함수)를 나타내며 x(t)x(t)는 그 신호들의 합으로 이루어진다는 것을 알 수 있습니다. cnc_n은 각 주기에서의 신호의 진폭을 나타냅니다.
그런데 이 Fourier Series는 주기를 가진 신호에 대해서만 적용할 수 있다는 점이 한계점입니다. 현실에는 주기를 갖지 않는 신호도 많이 존재하고 있는데, 그런 신호까지도 분석할 수 있도록 나온 개념이 바로 Fourier Transform입니다.

Fourier Transform

Fourier Transform은 위에서 설명 드린 것처럼 주기 신호에만 적용 가능하던 Fourier series를 비주기 신호까지 확장한 방법입니다.
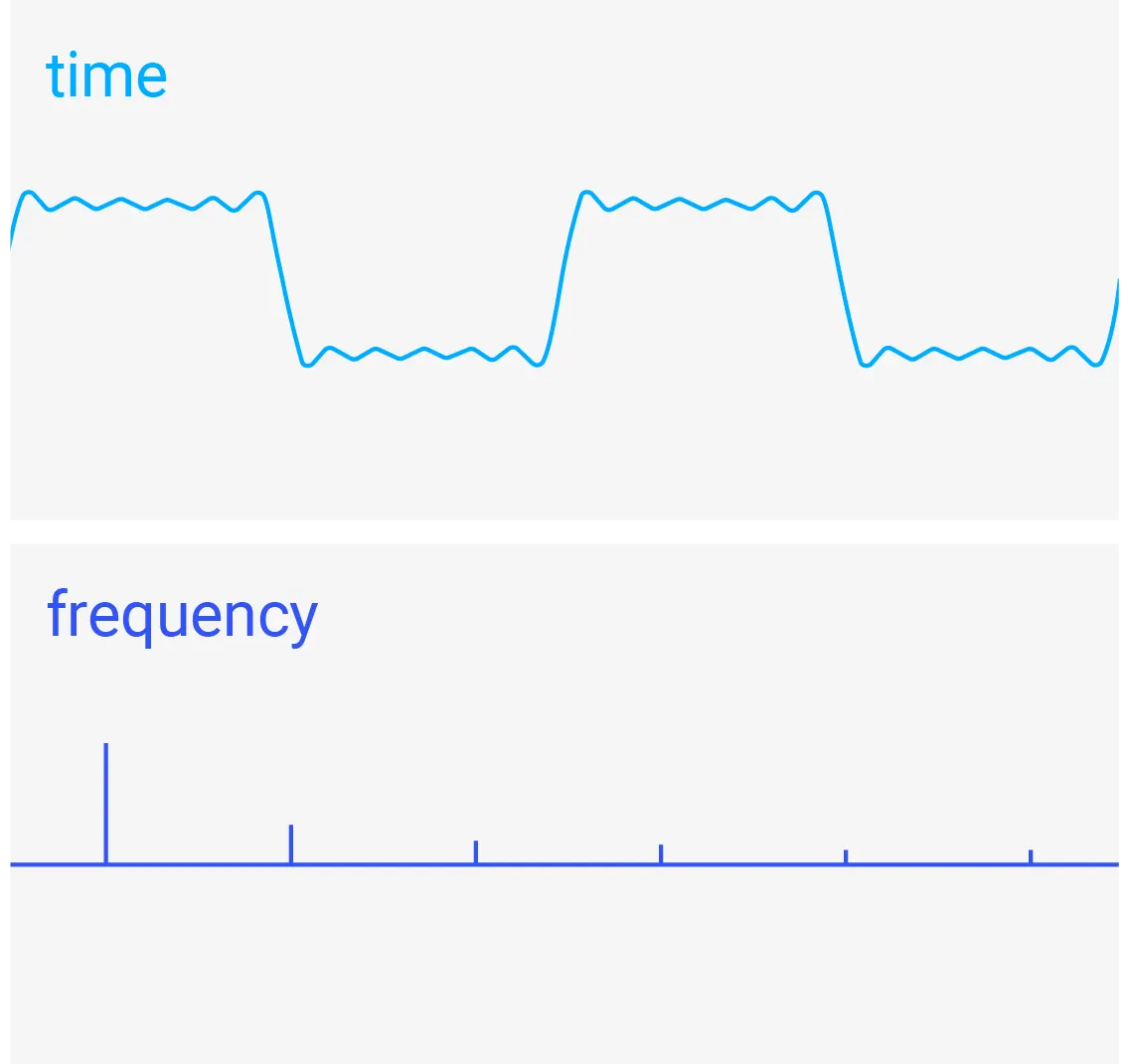
푸리에는 규칙적인 주기를 갖고 있지 않는 신호의 정보까지도 알아내기 위해 일단 주기가 매우 크다고(무한대)에 가정하여 어떤 신호라도 주기가 있다고 간주했습니다. 그 후에 모든 신호를 시간의 영역이 아닌 주파수의 영역으로 전환해서 보았는데요, 그 결과 주파수별로 개별 신호를 구분할 수 있게 되었습니다.
그림 4. (위) 시간 영역에서의 신호 그래프 (아래) 주파수 영역에서의 신호 그래프
위 내용을 수식과 함께 살펴보겠습니다. 신호의 주기가 무한대라면 위 Fourier series 진폭 cnc_n에 대한 수식이 다음과 같은 모양이 됩니다.
cn=lim⁡Tp→∞1Tp∫−Tp/2Tp/2x(t)e−j2π(n/Tp)tdtc_n = \lim_{T_p \to \infty} {1 \over T_p} \int^{T_p/2}_{-T_p/2} x(t) e^{-j2\pi (n/T_p) t}dt
지난 장에서 살펴본 바와 같이 주기의 역수는 주파수이므로(1/Tp=f)(1 / T_p = f) 수식을 조금 변형하면 아래와 같은 수식이 됩니다.
lim⁡△f→0(cn△f)=lim⁡Tp−>∞∫−Tp/2Tp/2x(t)e−j2π(n/Tp)t\lim_{\vartriangle f \rightarrow 0} ({{c_n} \over {\vartriangle f}}) = \lim_{T_p -> \infty} \int^{T_p/2}_{-T_p/2} x(t) e^{-j 2\pi (n/T_p)t}
이를 극한이 존재한다고 가정하면, 아래와 같이 적을 수 있습니다.
X(f)=∫−∞∞x(t)e−j2πftdtX(f) = \int^{\infty}_{-\infty} x(t) e^{-j2\pi ft}dt
X(f)X(f)는 주파수 f에 대한 진폭을 나타냅니다. 이 수식을 x(t)x(t)의 Fourier transform이라고 부릅니다. 이 수식을 이용해 시간에 대해 표현한 신호인 x(t)x(t)(그림 4, 위)를 주파수에 대한 신호 X(f)X(f)(그림 4, 아래)로 변환할 수 있게 됩니다.
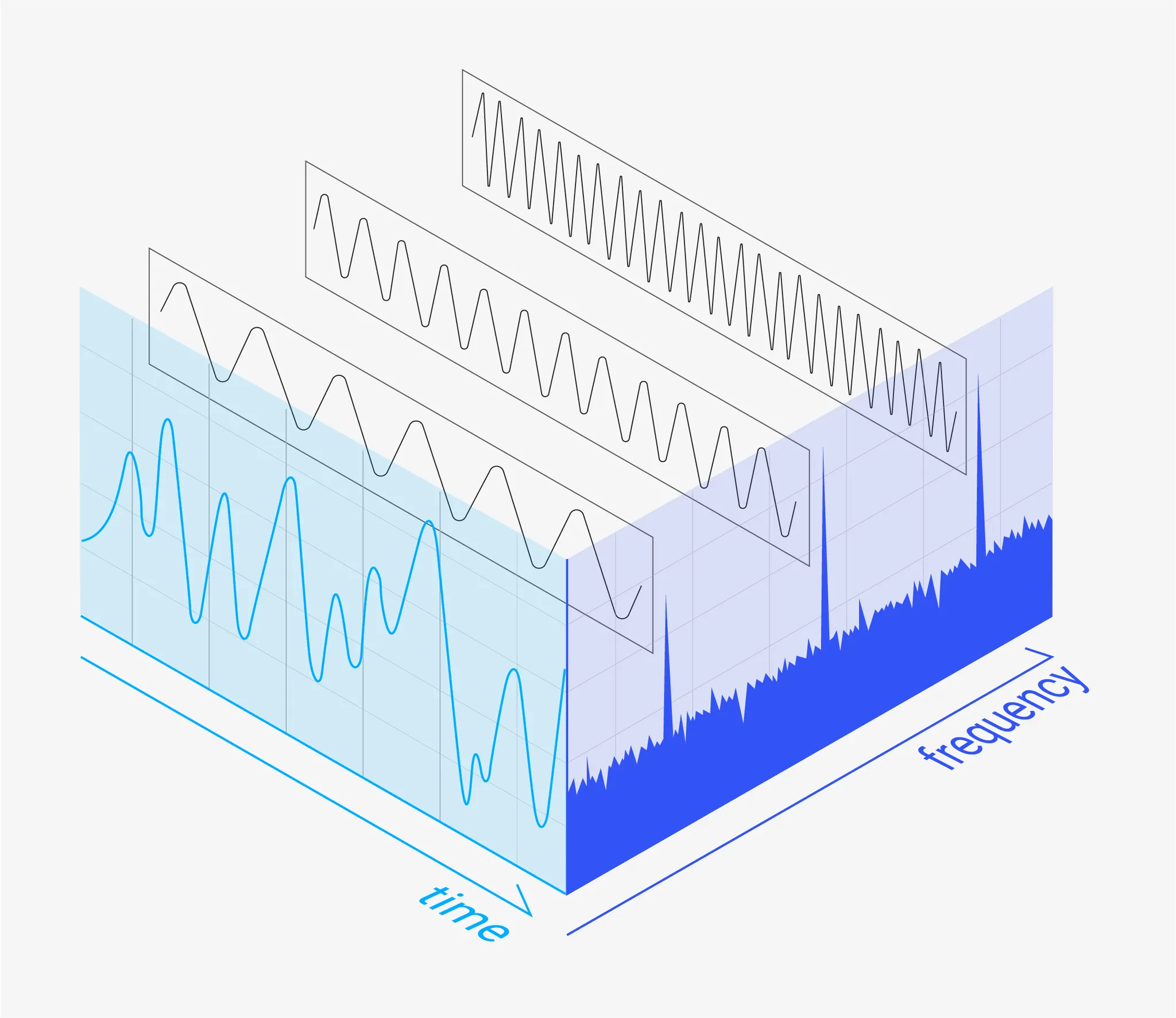
그림 5. (왼) 시간의 흐름에서 보는 신호 그래프 (오른) Fourier Transform을 통해 주파수 진폭에 따라 구분된 신호 그래프
위 그림과 같이 복잡한 신호를 단순한 신호들의 합으로 나눈 후, 주파수 영역에서 단순한 신호들의 주파수 특성을 분리해서 볼 수 있기 때문에 우리가 알고자 하는 복잡한 신호의 특성을 분석할 수 있게 됩니다.

DFT (Discrete Fourier Transform) & FFT (Fast Fourier Transform)

이 Fourier Transform에서 한 가지 저희가 놓치고 간 사실이 있는데 혹시 무엇인지 감이 오시나요?
바로 이 Fourier Transform이 가능하려면, 한 순간도 끊기지 않은 연속적인 데이터(continuous data)가 필요한데, 우리는 컴퓨터와 센서를 통해 ‘샘플링’된 이산 데이터(discrete data)만을 가지고 있다는 것이죠. 아무리 샘플링 주기를 짧게 설정해도 그 사이사이 추출되지 않은 정보가 존재하기 때문에, Fourier Transform을 바로 적용할 수 없는데요.
그래서 나온 또 다른 심화 개념이 Discrete Fourier Transform (DFT)입니다. 이름이 바뀌었지만 전혀 어렵지 않습니다. DFT는 기존 Fourier Transform 수식의 적분을 N개의 샘플에 대한 Sum으로 바꾼 형태이기 때문인데요. 이는 아래 수식과 같이 표현됩니다.
X(f)=∫−∞∞x(t)e−j2πftdtX(f) = \int^{\infty}_{-\infty} x(t) e^{-j2\pi ft}dt
X(k)=∑n=0N−1x[n]e−j2π(k/N)n    k=1,2,...,NX(k) = \sum^{N-1}_{n=0} x[n] e^{-j 2\pi (k / N)n}\ \ \ \ k=1,2,...,N
DFT 수식에서는 연속(continuous) 신호 x(t)x(t)를 샘플링된 이산(discrete) 신호 x[n]x[n]으로 표현하고, 연속 주파수인 ff 또한 이산 주파수 k/Nk/N으로 표현합니다. 이 수식을 통해 샘플링된 데이터도 Fourier Transform이 가능하게 됩니다.
자, 이제 정말로 변환을 해볼까 했더니, 우리가 가지고 있는 데이터 수가 엄청나게 많네요.
DFT 수식을 구현하면 시간 변수 nn과 주파수 변수 kk가 데이터 개수인 NN의 영향을 받기 때문에 시간 복잡도가 O(N2)O(N^2)이 됩니다. 데이터가 늘어나면 시간이 너무 많이 소요될 것 같은데… 방법이 또 없을까요?
이건 상대적으로 복잡한 문제는 아닙니다. 바로 Fast Fourier Transform (FFT)이라는 개념이 있기 때문이죠. FFT는 Divide and Conquer (분할 정복) 알고리즘을 활용해 계산 횟수를 줄여 계산 속도를 획기적으로 단축합니다. 이 방법을 통해서라면 시간 복잡도가 O(N2)O(N^2) -> O(NlogN)O(N logN)로 완화되기 때문에 빠르게 계산을 할 수 있습니다.
(FFT에 대한 자세한 내용은 링크를 참조하세요.)

Conclusion

분석하는 것이 불가능하다고 여겨졌던 복잡한 데이터를 진단하기 위해 끊임없이 한계점을 돌파하다 보니 어느새 4가지 개념 - Fourier Series, Fourier Transform, Discrete Fourier Transform, Fast Fourier Transform – 이나 알아볼 수 있었습니다.
하지만, Fourier Transform은 시간에 따른 주파수의 변화를 알 수 없다는 단점이 있습니다. 즉, 시간에 따라 주파수 특성이 변하는 신호가 있다고 했을 때, 그 시간 내에서 주파수가 어떻게 변했는지까지는 파악할 수 없다는 의미입니다.
그래서 다음 편으로는 시간-주파수 분석 기법을 통해 이와 같은 단점을 보완하는 방법을 설명해드리며 진동 신호 분석에 대한 여정을 이어가도록 하겠습니다.
신호 분석을 통한 기계 설비 진단 및 예측 시리즈 다음 편 보러가기
•
진동 신호를 사용한 기계 설비 고장 진단 및 예측: (2) 주파수 분석 방법을 이용한 진동 신호 분석

이 글을 쓴 사람

김 경 환 | 베타(β)팀
원프레딕트의 산업설비 솔루션 개발을 하고 있습니다.
AI 기술을 이용해 다양한 문제를 해결하는 소프트웨어 엔지니어입니다. 원활한 개발 협업을 위한 시스템을 구축하는 데에 관심이 많습니다.
게임을 하는 것도 좋아하고 보는 것도 좋아합니다. 현실도 게임처럼 매일매일 Level up!
오 혜 원 | 마케팅팀
원프레딕트 마케팅팀에서 홍보와 대내외 커뮤니케이션을 담당하고 있습니다.
천상 문과생이지만 최첨단 초일류 AI 회사에 다니는만큼 어디 가서 창피 당하지 않을 정도의 이과적 소양을 쌓고자 노력하는 중입니다.
물욕이 강한 편이라, 하고 싶은 거, 입고 싶은 거, 먹고 싶은 거 다 사기 위해 오늘도(뚠뚠) 개미는(뚠뚠) 열심히(뚠뚠) 일하고 있습니다.
원프레딕트 홈페이지 https://onepredict.ai/
원프레딕트 블로그 https://blog.onepredict.ai/
원프레딕트 기술 블로그 https://tech.onepredict.ai