홈
⚙️

시계열 데이터를 사용한 기계 설비 고장 진단 및 예측: 4) 구름요소 베어링 진단에의 적용

지난 3편에서는 Fourier Transform, Wavelet Transform 등 기본적인 주파수 분석 방법에 대해 알아보았습니다. 이어서 이번 장에서는 이런 방법들을 활용해 구름요소 베어링을 진단하는 과정 및 그에 수반되는 부가적인 기법에 대해 소개하고자 합니다.
<진동 신호를 사용한 기계 설비 고장 진단 및 예측> 시리즈 전편 보러가기

Intro.

베어링이란 ‘회전운동을 하는 축을 일정한 위치에서 지지하여 운동을 제한하고 마찰을 줄여주는 기계요소’를 지칭합니다. 이러한 베어링은 거의 모든 회전체 설비에 포함되어 있기 때문에, 회전체를 진단하기 위해서는 베어링 진단이 가장 필수적으로 진행되어야 합니다.
저희 원프레딕트에서도 GuardiOne Bearing을 통해 베어링에서 측정된 진동 데이터를 산업AI를 통해 분석하고 베어링의 상태와 고장을 진단하는 솔루션을 제공하고 있습니다. 이번 장에서는 원프레딕트가 베어링 고장 진단에 이용하는 신호처리 기법 중 일부 방법에 대해 다뤄보려고 합니다.
*추후 본 글에서 베어링이라 하면 구름요소 베어링을 이야기합니다.
*보다 명료한 설명을 위해 표준 공개 데이터셋 중 하나인 CWRU (Case Western Reserve University)의 베어링 데이터셋을 예시로 활용할 예정입니다. 해당 데이터셋은 CWRU 베어링 데이터 센터 (웹페이지 링크)에서 다운로드 받을 수 있습니다.

베어링 고장 진단 프로세스

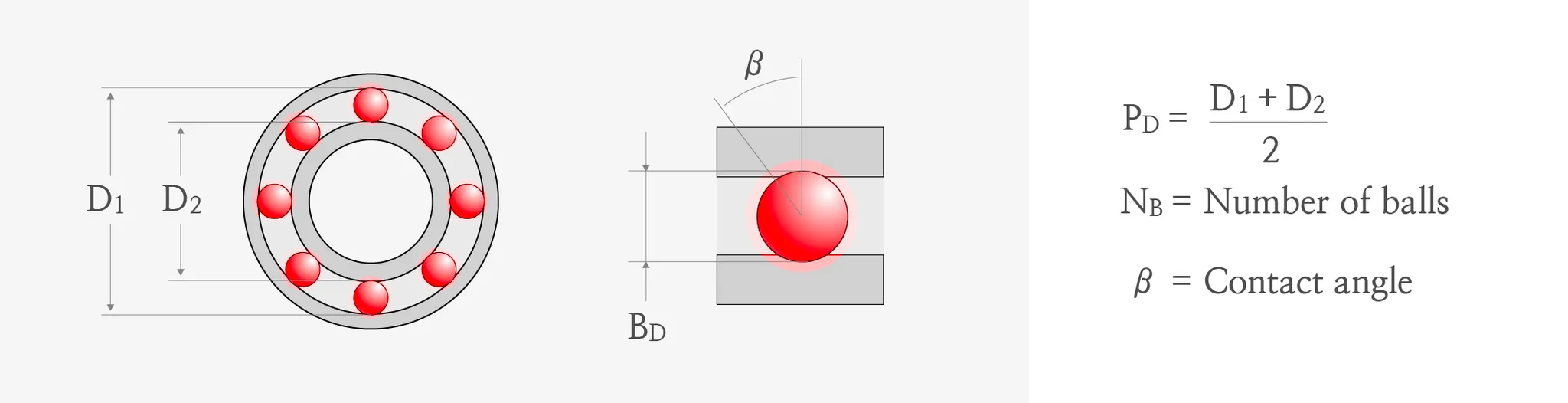
그림 1. 구름요소 베어링의 구조
위 그림 1과 같은 베어링의 고장 진단 프로세스는 아래와 같이 정리될 수 있습니다.
1) 베어링 고장 특성 주파수 도출
2) 정상신호 억제, 고장신호 증폭 (선택적)
3) 잡음 제거
4) 고장신호 분리
5) 주파수 분석
6) 진단

AR-MED Filter

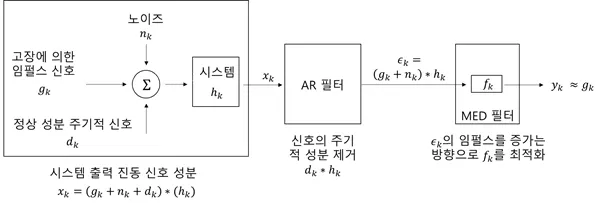
해당 내용을 이해하기 위해서는 LTI 시스템에 대한 기본적인 이해가 필요하지만, 상황에 따라 바로 다음 항목인 Spectral Kurtosis로 넘어가도 무관합니다.
AR-MED 필터는 아래 그림과 같이 autoregressive (AR) 필터와 minimum entropy deconvolution (MED) 필터가 직렬로 연결된 필터로, 신호가 가지는 정상성분은 억제하고, 고장성분을 증폭시켜 줌으로써, 고장신호가 더 도드라지게 해 줍니다.
아래 그림을 통해 AR-MED 필터의 원리 및 특성을 한눈에 확인할 수 있습니다. 이어지는 설명은 해당 그림을 따라가며 진행하겠습니다.
그림 2. AR-MED 필터
 먼저, 그림 좌측부에 시스템으로의 입력 및 그에 따른 시스템으로부터의 출력의 생성 과정이 표현되어 있습니다. LTI 시스템이라는 가정 하에, 고장에 의한 임펄스 신호 gkg_k, 노이즈 신호 nkn_k, 정상성분신호(주기적) dkd_k 의 복합적인 입력에 대한 시스템의 출력은 xk=(gk+nk+dk)∗hk x_k=(g_k+n_k+d_k )*h_k 로 표현됩니다.
(여기서 *는 convolution연산을 의미하며, hkh_k는 시스템 고유의 임펄스 응답 함수를 의미합니다. 이해가 되지 않는다면 LTI 시스템 및 LTI 시스템의 입출력에 대해 공부하여 볼 것을 추천합니다.)
우리가 진동센서를 통해 관측하는 신호는 바로 이 xk x_k 입니다.
 이어서, 그림 중앙부의 AR 필터는 아래 식과 같이 시점 k에서의 값을 k−1k-1 ~ k−pk-p 에서의 총 pp개의 관측치를 이용하여 주기적인 부분을 선형회귀하며, 나머지 비주기적인 노이즈를 ϵkϵ_k로 설명하는 AR 모델을 이용해 모델링합니다.
이 과정에서 xkx_k의 dk∗hkd_k*h_k는 선형회귀 부분에, 나머지 (gk+nk)∗hk(g_k+n_k)*h_k는 ϵk ϵ_k 에 의해 모델링이 되었다고 가정합니다.
(여기서 주의할 할 점으로, 필터의 길이를 나타내는 p를 관측하고자 하는 고장성분의 주기보다 짧게 가져가야 한다는 점으로, 고장에 의한 주기적인 성분이 AR 모델링의 선형회귀 부분에 포함되지 않도록 해야 합니다.)
주기적인 정상성분은 억제하고자 하기 때문에, AR 필터는 ϵkϵ_k만을 출력으로 내보냅니다.
x[k]=∑i=1paix[k−i]+ϵkx[k]=\sum_{i=1}^{p} a_ix[k-i]+ϵ_k
 마지막으로, 그림 우측의 MED (Minimum Entropy Deconvolution) 필터는 어떤 혼합된 출력신호로부터 임펄스 입력을 추출해내는 필터입니다. 하지만, 실제 물리적으로 존재하는 시스템을 정확히 모델링하여 그 역을 찾아주는 접근도, 실제 입력치와 필터 출력을 비교하여 필터 계수를 점진적으로 학습시키는 접근도 현실적이지 않을 것입니다. 따라서, MED 필터는 자신의 출력의 kurtosis가 최대화되도록 필터 계수를 조절함으로써 임펄스 입력을 추정, 복원합니다.
(여기서 kurtosis란 분포의 뾰족한 정도, 즉 신호의 임펄스의 정도를 나타내어 주는 통계량으로, 이에 대한 설명은 아래 Spectral Kurtosis 항목에서 다시 나오니 여기서는 그냥 넘어가겠습니다)
사실 kurtosis가 최대화된 출력을 입력신호의 근사치로 본다는 점에 어느정도 비약이 있어 보이지만, 그렇다고 아예 말이 안 되는 것도 아닙니다. 결국, AR-MED 필터에서, MED 필터는 그림과 같이 AR 필터의 출력인 ϵ_k를 입력으로 받아 임펄스 입력신호 g_k를 추정, 복원해내는 역할을 수행합니다.
이제, ‘minimum entropy deconvolution’의 의미가 드러납니다. 노이즈 nkn_k 부분을 삭제해주고, 임펄스에 의한 신호 gkg_k 부분만을 남겨 줌으로써 신호가 가지는 엔트로피를 감소시켰다고 할 수 있으며, 입력신호와 시스템의 임펄스응답함수의 convolution으로 표현되는 출력으로부터 역으로 입력신호를 찾는다는 점에서 convolution의 역인 deconvolution이라는 이름이 붙은 것을 알 수 있습니다.
필터의 계수를 탐색하는 과정에 대해서 관심 있으신 분들은 개별적으로 확인 부탁드립니다.
위에서 살펴본 AR 필터와 MED 필터를 통과하여 나온 신호는 정상성분이 억제되고, 고장성분이 극대화된 신호라고 볼 수 있습니다. 우리는 이것이 입력 고장신호를 근사 한다고 여기고 추후 분석에 이용합니다.

Spectral Kurtosis

앞서 설명한대로, 전체 신호에서 분석하고자 하는 베어링 관련 신호만 남기고 나머지는 제외하기 위해 베어링의 고유 진동수에서 대역 필터링을 해주어야 합니다. 보통 스펙트럼 상에서 2 ~ 5 kHz 정도 구역을 관찰하고, 그 중 도드라지는 부분을 필터링 대역으로 채택하지만, 경우에 따라서는 그 결정이 다소 막막할 수 있습니다.
이를 해결하기 위해 Spectral Kurtosis (SK) 기법을 이용할 수 있습니다.
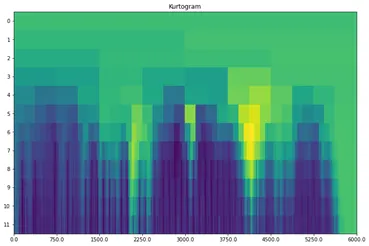
SK는 보통 아래 그림 3과 같은 kurtogram의 형태로 표현됩니다. 그림에서 확인할 수 있듯이, kurtogram의 수평축은 주파수 영역, 수직축은 level을 나타냅니다. 여기서 level은 스펙트럼 분할의 정도를 의미하는데, level이 한 단계씩 깊어질수록 스펙트럼은 2배씩 분할되므로, levelN(N:0,1,2,…) level N (N: 0,1,2, …) 에서의 분할 구간의 갯수는 총  개, 길이는 (samplingfrequency/2)/(2N)(sampling frequency/2)/(2^N) 이 됩니다. Kurtogram의 각 구간에는 해당 구간의 주파수 대역에서 대역 필터링된 신호의 kurtosis 값이 계산되어 들어갑니다.
그림 3. 전형적인 kurtogram의 형태
kurtosis란 아래 수식과 같이 표현되는 통계량으로, 특정 분포의 뾰족한 정도를 나타내어 줍니다.
(이 경우에는 해당 주파수대역에서 필터링 된 시계열 신호의 형태가 얼마나 평평하거나 뾰족한 지를 의미합니다. 다음 단락에 이에 대한 예시가 나옵니다.)
kurtosis:∑n=1Ny4[n][∑n=1Ny2[n]]2kurtosis:\frac{\sum_{n=1}^{N}y^4[n]}{[\sum_{n=1}^{N}y^2[n]]^2}
베어링의 결함에 의해 발생하는 임펄스 신호는 아래 그림 4와 같이 신호상의 스파이크들을 만들기 마련입니다. 이러한 신호는 높은 kurtosis값을 가지므로, kurtogram상에서 부각됩니다.
따라서, 우리는 kurtogram상에서 도드라지는 부분을 관찰하여, 해당 구간이 고장에 의한 임펄스 신호를 많이 포함한 구간이라 생각하고, 이를 필터링 대역으로 선정합니다.
아래 그림 5에서 신호의 형태와 kurtosis 값을 비교함으로써 신호의 형태와 kurtosis값 사이의 관계를 이해할 수 있습니다.
그림 4. 베어링 고장 시 Timeseries
그림 5. Kurtosis와 Timeseries
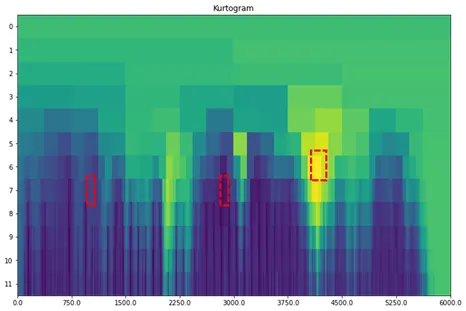
그림 5와 같이, CWRU 데이터셋의 경우 4100~4250 Hz 정도에서 kurtosis 값이 가장 높았습니다.
따라서, 해당 구역에 고장신호가 가장 많이 포함되어 있다고 가정하고, 이에 대해 대역 필터링을 진행합니다.

Hilbert transform을 통한 포락선 추출

진폭 변조(Amplitude Modulation: AM)는 어떤 신호 m(t)(messagesignal) m(t) (message signal) 와 sin(t),cos(t)sin(t), cos(t)등의 주기성을 갖는 신호 (carrier signal) 가 곱해졌을 때 발생하는 현상입니다.
진폭 변조된 신호를 시간 도메인에서 보면 아래 그림 6의 예시와 같이 message signal 이 carrier signal에 의해 표현되는 꼴로 나타납니다. 다시, 진폭 변조된 신호를 주파수 영역에서 보면 아래 그림 7와 같이 carrier signal 중심으로 양쪽에 2개의 주파수 성분이 생기는 sideband형태가 나타나게 됩니다.
그림 6. Amplitude modulation example
그림 7. Amplitude modulation → sideband
앞서 베어링에 국부적인 결함이 발생할 경우, 베어링 볼이 해당 부분을 치고 지나가면서 임펄스 신호를 발생시킨다고 하였는데, 이 임펄스 신호는 아래 그림 8에서와 같이 베어링의 고유 진동수에 의해 진폭 변조된 채로 발생합니다.
(임펄스 신호와 고유진동수의 정의에 대해 고민해 보면 이 부분이 직관적으로 와 닿을 것입니다.)
그림 8. CWRU 데이터셋 임펄스 신호
현재 우리가 분석해야 할 신호는 베어링 결함에 의한 임펄스 신호입니다. 그런데, 고유진동수에 의해 진폭 변조된 신호를 그대로 주파수 분석하면 앞서 언급한 것과 같이 임펄스 신호가 sideband의 형태로 존재할 것이므로, 원활한 분석을 위해 임펄스 신호만을 분리해내어 Fourier Transform을 진행하여야 합니다.
일반적으로, 그 분리 방법으로 Hilbert Transform을 통한 포락선 추출을 이용하는데, 그 과정은 아래 수식으로 나타낼 수 있습니다.
xenv(t)=∣x(t)+jx^(t)∣x_{env}(t)=|x(t)+j\hat{x}(t)|, wherex^(t)=1π∫−∞∞x(t)dτwhere\hat{x}(t)=\frac{1}{π}\int_{-∞}^{∞}{x(t)dτ}
Hilbert Transform을 진행할 경우, 아래 그림 9의 주황색 선과 같이 임펄스 신호의 형태를 지닌 선을 추출할 수 있습니다. 이 선은 포락선(envelope)으로 지칭되며, 고유진동수가 제외된 임펄스 신호만을 포함하고 있습니다.
그림 9. CWRU 데이터셋 포락선 추출
신호에서 포락선를 추출한 이후 FT하면 아래 그림 10과 같이 베어링의 국부적인 고장에서 발생하는 임펄스 신호의 주파수 성분, 즉 BPF 및 그 harmonics를 확인할 수 있습니다. 그림 10에 사용된 CWRU 데이터셋 예시의 경우, 외륜 결함(OR Fault)이 존재하며 앞서 언급된 것과 같이 이론적 BPFO가 약 104 Hz 정도이므로, 104 Hz 및 그 배수의 위치에서 성분이 존재하는 것을 확인할 수 있습니다.
그림 10. CWRU 데이터셋의 (위) 기본(raw) 스펙트럼, (아래) 포락선(envelope) 스펙트럼

Conclusion

이번 장에서 설명한대로 베어링 고장 신호를 분석하기 위해서는 SK기법을 이용한 대역 필터링, Hilbert Transform을 이용한 envelope 추출등의 과정을 거쳐야 합니다.
전체 과정을 한눈에 나타내어 보면 아래 그림 11과 같습니다.
그림 11. 원신호 – 대역 필터링 – envelope 추출 – FT 과정
이번 글에서는 베어링 진단의 프로세스 및 진단을 위해 자주 사용되는 Hilbert transform, spectral kurtosis에 대해서 간단히 살펴보았습니다.
베어링의 경우 CWRU, IMS 등 무료로 오픈 되어 있는 데이터셋이 다수 존재하기 때문에, 직접 프로세스를 밟아보며 기법들을 사용해본다면 이해하는 데 더 도움이 될 것 같습니다.
신호 분석을 통한 기계 설비 진단 및 예측 시리즈 이전 편 보러가기
•
진동 신호를 사용한 기계 설비 고장 진단 및 예측: (4) 구름요소 베어링 진단에의 적용

이 글을 쓴 사람

유 재 원 | 베타(β)팀
진단알고리즘 개발을 맡고 있는 유재원입니다.
새로운 기술적인 것을 배우는 데에 관심이 많습니다.

이 글을 정리한 사람

오 혜 원 | 마케팅팀
원프레딕트 마케팅팀에서 홍보와 대내외 커뮤니케이션을 담당하고 있습니다.
천상 문과생이지만 최첨단 초일류 AI 회사에 다니는만큼 어디 가서 창피 당하지 않을 정도의 이과적 소양을 쌓고자 노력하는 중입니다.
물욕이 강한 편이라, 하고 싶은 거, 입고 싶은 거, 먹고 싶은 거 다 사기 위해 오늘도(뚠뚠) 개미는(뚠뚠) 열심히(뚠뚠) 일하고 있습니다.
원프레딕트 홈페이지 https://onepredict.ai/
원프레딕트 블로그 https://blog.onepredict.ai/
원프레딕트 기술 블로그 https://tech.onepredict.ai