🎱

Uncertainty와 Bayesian, 그리고 Monte Carlo Dropout

Uncertainties in Deep Learning Algorithms

현대의 딥러닝 알고리즘들은 여러층의 non-linearity와 효과적인 optimization 방법들을 통해서 강력한 representational learning capability와 generalization 성능을 얻게 되었습니다. 그럼에도 우리가 잊으면 안되는 점, 뉴럴넷들은 단지 학습 데이터에 fitting이 되어있는 상태에서 사용된다는 사실입니다.

다시 말해서, 우리는 학습 데이터에서 보지 못한, 혹은 학습 데이터의 분포와 다른 분포를 갖는 예측 데이터에 대해서 뉴럴넷이 정확하게 예측을 하는지에 대해서는 의문을 가질 필요가 있습니다. 테슬라를 비롯한 자동차 업체들의 자율주행 기능이 아직도 완전히 신뢰 받지 못하는 이유도 이것 때문이라고 볼 수 있습니다.

이러한 경우에 우리가 할 수 있는 방법은, 딥러닝 모델의 예측에 대한 불확실성, 즉 uncertainty를 정량화하는 것입니다. 이 경우, 모델이 자주 보지 못한 패턴의 예측데이터일수록 모델의 예측값에 대한 uncertainty가 높게 나올 것이고, 이를 바탕으로 의사결정에서 얼마나 딥러닝 모델에 의지할 지를 결정할 수 있습니다. 학습 데이터가 충분하지 않은 경우나, 모델의 안전성이 중요한 메디컬, 산업 AI분야에서 uncertainty를 고려하는 것은 더욱 중요한 문제가 됩니다.

Bayesian Deep Learning

그렇다면 딥러닝에서 uncertainty를 어떻게 표현할 수 있을까요? 가장 기본적인 방법은 Bayesian 기반의 모델링을 하는 것입니다.

여기서 말하는 Bayesian이란 무엇일까요? 통계학으로 세상을 바라볼 때 우리가 취할 수 있는 두 가지 다른 접근법이 있습니다. 바로 Frequentist로서의 접근법과 Bayesian의 접근법입니다. Statistics: Are you Bayesian or Frequentist? 두 관점의 차이를 간략히 설명하자면, Frequentist들은 오로지 관측된 데이터만을 고려하여 어떠한 분포에 대한 예측을 하는 반면, Bayesian들은 관측된 데이터 저변에 깔려있는 prior distribution을 고려하여 예측을 한다는 점이 다른 점입니다. 이 경우 Frequentist들의 관심을 가지는 값은

p(D|\theta)

, 즉 likelihood인 반면, Bayesian들의 관심 가지는 값은 prior distribution이 고려된

p(\theta|D) = \frac{p(D|\theta)p(\theta)}{p(D)}

, 즉 posterior distribution이라고 볼 수 있습니다.

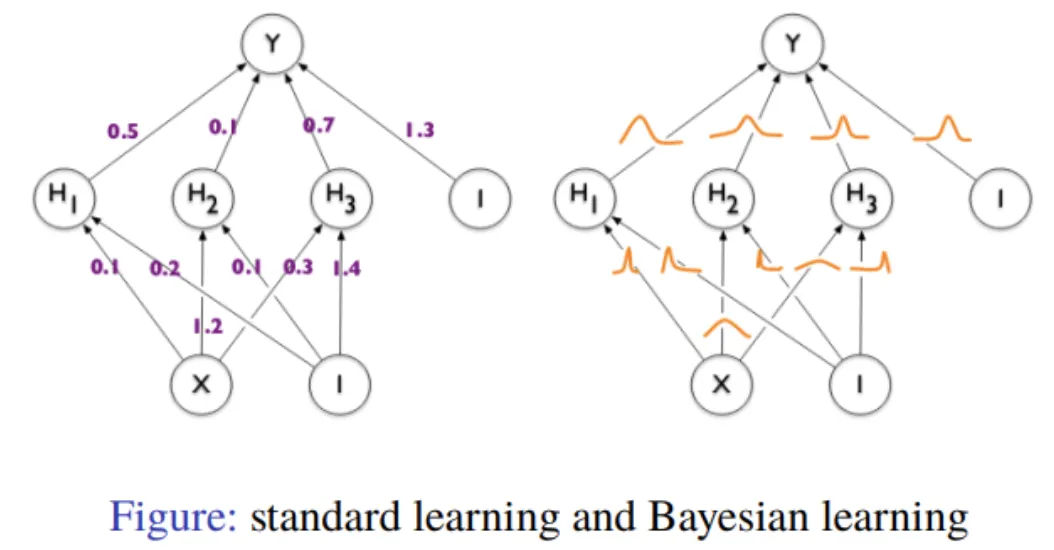
그림 1. Standard machine learning and Bayesian learning

기존 머신러닝, 혹은 딥러닝 모델들은 하나의 input에 대해 하나의 output, 즉 point estimate 을 하는 방식이었습니다. 좀더 디테일하게 설명해보자면, 우리가 지금 돌리고 있는 Deep learning은 대부분

\underset{\theta} {\mathrm{argmax}} [p(D|\theta)]

를 만족하는 '하나의' weight point

\theta

를 찾는 문제입니다. 위와 같은 방식을 maximum likelihood estimation(MLE)이라고 합니다.

반면, 앞에서 말씀드렸듯 Bayesian들의 관심은

p(\theta|D) = \frac{p(D|\theta)p(\theta)}{p(D)}= \frac{p(D|\theta)p(\theta)}{\int_{\theta'}p(D, \theta')d\theta'}

로 정의되는 posterior probability 그 자체를 구하는 것입니다. 혹은 이 posterior probability에서 sampling해서 예측값들의 분포를 구하는 것이라고 볼 수도 있겠죠. Bayesian learning 은 하나의 input에 대해 여러번의 output을 얻고, 이 여러 output들의 분포를 구해볼 수 있습니다. 이 경우 output들의 분포에서 나오는 분산값을 uncertainty로 정의할 수 있습니다.

Overconfidence Problem

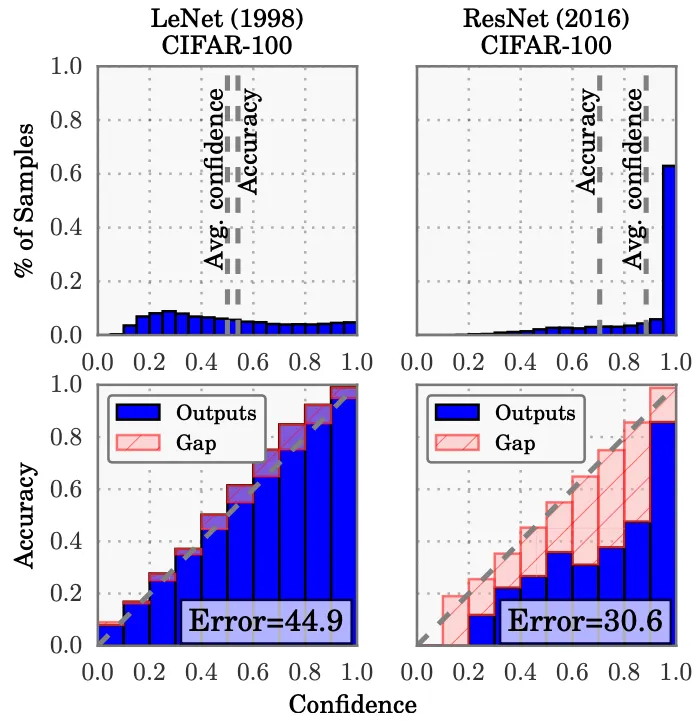
모델의 uncertainty를 정량화 하는 것 이외에도, 대다수의 Bayesian deep learning 방법들은 기존 딥러닝 모델에 적용했을 때 overconfidence 문제를 완화해준다고 알려져 있습니다. 모델의 예측값이 정확한 것도 중요하지만, 동시에 예측값이 실제 확률을 반영하는 것 역시 중요하며 이를 calibration이라고 합니다. 현대의 뉴럴넷은 정확도는 향상되었지만 지나치게 overconfident한 예측값을 보여주면서 calibration 성능이 매우 나빠지는 경향이 있습니다.

그림 2. Well-calibrated model(left) and overconfident model(right)[1]

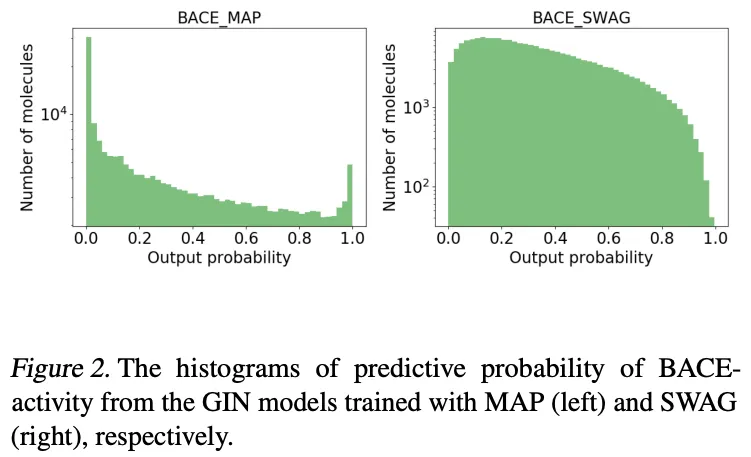
Overconfidence 문제를 해결하는 방법으로 temperature scaling 등 예측값의 logit 자체를 튜닝하는 여러 방식들이 제안되어 왔지만, Bayesian deep learning 방식을 적용하는 것이 이를 온전하게 해결한다는 연구들이 여럿 있어 왔습니다. 아래 그림에서도 볼 수 있듯이, 기존 방식(BACE_MAP)에서의 예측 logit값이 0 혹은 1에 지나치게 몰려 calibration 성능이 나쁜 경우에 Stochastic Weight Averaging-Gaussian 이라는 Bayesian deep learning 방법을 적용함으로써 예측 logit값들이 고른 분포를 보이면서 overconfidence문제가 해결됨을 알 수 있습니다.

그림 3. Overconfident vanilla deep learning model(left) and Well-calibrated Bayesian deep learning model(right)[2]. 왼쪽에서 기존 딥러닝 방식으로 예측된 predictive probabilities, 즉 어떠한 예측이 True일 확률에 대한 예측값들이 0 혹은 1에 쏠려있는 것 과 비교하여, 오른쪽에서 Bayesian deep learning의 경우 predictive probabilities가 훨씬 더 부드럽고 자연스러운 분포를 그리고 있음을 볼 수 있습니다.

Monte Carlo Dropout

Bayesian deep learning의 방법에는 여러가지가 있습니다만, 가장 널리 사용되고 편하게 쓸 수 있는 것 중 하나가 MC (Monte Carlo) dropout[3]입니다. MC dropout에서는 각 dropout layer을 활성화시켜 모델을 학습합니다. 그리고 일반적인 dropout과 달리, inference시에도 dropout을 활성화시켜 여러번의 output을 뽑습니다. 이 경우 나온 output들의 분포를 Posterior probability에서 sampling된 분포로 보고, 이 분포를 통해서 Bayesian 모델링 관점에서의 uncertainty를 계산할 수 있다는 것이 Monte Carlo Dropout의 골자입니다. Yarin Gal님이 쓴 아래 논문이 이에 대한 증명을 하고 있습니다.

Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning

(이 논문 외에도 Yarin Gal님이 쓰신 논문중에는 Bayesian deep learning과 관련해서 읽어볼만한 논문들이 많습니다.)

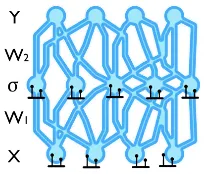
그렇다면 MCdropout을 구체적으로 어떻게 써야될까요? Pytorch 예시 코드와 함께 설명드리겠습니다. 먼저, 기본적인 모델링은 다음 그림과 같이 마지막 output layer직전의 모든 activation layer 뒤에 dropout layer 를 추가하는 방식입니다.

그림 4. Bayesian neural network with dropout[4]

self.layer1 = nn.Sequential(
            nn.Linear(in_features, out_features, bias=True),
            nn.BatchNorm1d(out_features),
            nn.ReLU(),
            nn.Dropout(p=1 - keep_prob)
        )
Python
복사

그리고 다른 딥러닝 방식과 동일하게 optimization을 진행하시면 됩니다. 단, Loss의 경우 다음과 같이 정의됩니다.

\mathcal{L} = -\sum_{n=1}^{N}\text{log }p(y_n|x_n, \hat{\theta}^n)+\lambda||\theta||^2

여기서 주의할 점은, 여기에서 쓰이는

\lambda||\theta||^2

는 L2 regularization에서 나온것이 아니고 Bayesian deep learning관점에서의 optimization 유도 과정에서 나온 부분이므로 생략하시면 안됩니다. 보통 pytorch의 경우 optimizer의 argument에 weight_decay 값에 작은 값을 넣어주고 사용하시면 됩니다. 여기서 한 가지 고려할 점은, 하나의 layer 안에서 Batch normalization과 dropout을 같이 쓸때의 순서에 대해서는 아직 갑론을박이 많습니다. 현재까지는 1) 가능하면 둘을 같이 쓰지는 말되, 2) 굳이 같이 써야된다면 batchnorm을 matrix multiplication 바로 뒤에, dropout은 non-linearity 바로 뒤에 적용하는 식으로 하는 것이 그나마 낫다 라는 의견이 가장 지배적입니다[5].

이제 모델이 충분히 학습이 된 후 test data에 대해서 inference를 진행해봅시다. inference 과정은 다음과 같습니다.

with torch.no_grad():
    model.train()
    mc_samples = 10
    predictions = []
    for X_test, Y_test in test_dataloader:
        pred_i = []
        for _ in range(mc_samples):
            pred_i.append(model(X_test))
        predictions.append(torch.stack(pred_i, dim=1)) 
    predictions = torch.cat(predictions, dim=0) 
		# N instances x N samples x N classes

    mean_pred = torch.mean(predictions, dim=1)
    mean_var = torch.var(predictions, dim=1)
Python
복사

Inference 과정의 요지는 1) dropout layer를 activate 시킨 상태에서 (Pytorch에서는 model.train()) 2) 정의된 Monte Carlo sample 개수만큼 prediction값을 sampling(for _ in range(mc_samples): 부분) 두 스텝이라고 보시면 되고 sample 개수만큼 나온 예측값들의 mean 값, variance 값을 이용하는 방식이라고 보시면 됩니다.

Conclusion

MC dropout은 구조가 매우 간단하고, 기존 모델을 크게 수정할 필요도 없으며, 대부분의 딥러닝 모델에 적용이 가능하다는 점에서 Bayesian deep learning을 적용할 때 가장 기본이 되는 baseline 모델로 활용하기 좋습니다. 다만, inference 과정에서 MC sample번 만큼 inference 과정을 반복해야한다는 문제점이 있습니다. 예를 들어 inference 과정에서의 time cost가 큰 모델이라던가, 아니면 inference가 실시간으로 이뤄져야하는 경우에 이는 큰 문제가 될 수 있겠죠. 최근에 이러한 문제를 해결하려는 논문[6]도 있었는데 상당히 흥미로웠던 기억이 있으니 읽어보셔도 좋을 것 같습니다.

MC dropout 외에도 여러 Bayesian deep learning 관련 연구가 진행되고 있고 좋은 논문들이 많이 나오고 있으니 딥러닝의 Uncertainty와 관련된 접근법들에 대해서 한번쯤 공부해보시면 Real world 문제를 해결함에 있어서 좋은 무기가 될 수 있을 것입니다.

이상으로 이번 글을 마치겠습니다. 감사합니다.

[References]

[1] Guo et al., "On Calibration of Modern Neural Networks", ICML 2017 [2] Hwang et al., "A benchmark study on reliable molecular supervised learning via Bayesian learning", ICML UDL 2020 [3] Gal et al., "Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning", ICML 2016 [4]https://www.cs.ox.ac.uk/people/yarin.gal/website/blog_3d801aa532c1ce.html [5] Li et al., "Understanding the Disharmony Between Dropout and Batch Normalization by Variance Shift", CVPR 2019 [6] Brach et al., "Single Shot MC Dropout Approximation", ICML UDL 2020

이 글을 쓴 사람

황 도 영 | 감마 팀

많이 아는거보다는 부딪히고 허슬하는게 더 중요하다고 생각하는 사람입니다.

원프레딕트에서 산업용 로봇 진단 솔루션을 개발하고 있습니다. 주말엔 그냥 직장인밴드 갔다가 기타치다가 베이스치다가 누워서 자구요...지금도 자고싶습니다. 허슬링은 회사에서만...

원프레딕트 홈페이지 https://onepredict.ai/

원프레딕트 블로그 https://blog.onepredict.ai/

원프레딕트 기술 블로그 https://tech.onepredict.ai