🧵

연속 웨이블릿 변환의 원리와 구현

Introduction

회전하는 여러 설비들 중에는 정속으로 회전하는 설비들도 있지만, 속도가 변하는 설비들도 많습니다. 예를 들어 산업용 로봇의 경우 6개의 축에 있는 각 서보모터들이 순간적으로 가속되었다가 감속되면서 제어됩니다. 즉, non-stationary한 상태로 가동됩니다.

회전설비의 진단을 위해 고장으로 인한 특성 주파수를 추출이 필요합니다. 그런데 이런 가변 속도 설비들의 경우 고장의 특성을 추출하기 위해서는 시간에 따라 주파수 특성이 변하기 때문에 그 변화를 포착할 수 있어야 합니다. 그렇기 때문에 Onepredict에서는 산업용 로봇의 고장 특성을 보기 위해 CWT(Continuous Wavelet Transform, 연속 웨이블릿 변환)을 사용해 전처리 과정을 갖습니다.

이번 글에서는 CWT의 원리에 대해 더 자세히 살펴보고, 직접 코드로 구현해보도록 하겠습니다.

Concept and Principle

웨이블릿 변환(Wavelet Transform)은 임의의 신호를 웨이블릿(Wavelet)으로 정의되는 함수들로 분해하는 방법입니다. 푸리에 변환(Fourier Transform)이 무한히 진동하는 sine, cos 함수를 기저함수로 사용해 신호를 분해나는 것과는 달리 웨이블릿 변환은 진동하는 시간이 제한되는 함수를 기저함수로 사용해 시간 당 포함되는 주파수 성분의 크기를 보게 됩니다.

그 원리도 어렵지 않은데요. 원리를 요약하자면 특정한 규칙에 따라 모델링 된 웨이블릿 함수의 시간 스케일을 바꿔가며 원본 신호와의 상관 계수를 계산해 변환할 수 있습니다. 그 과정을 한 번 차근차근 살펴보겠습니다.

웨이블릿(Wavelet)

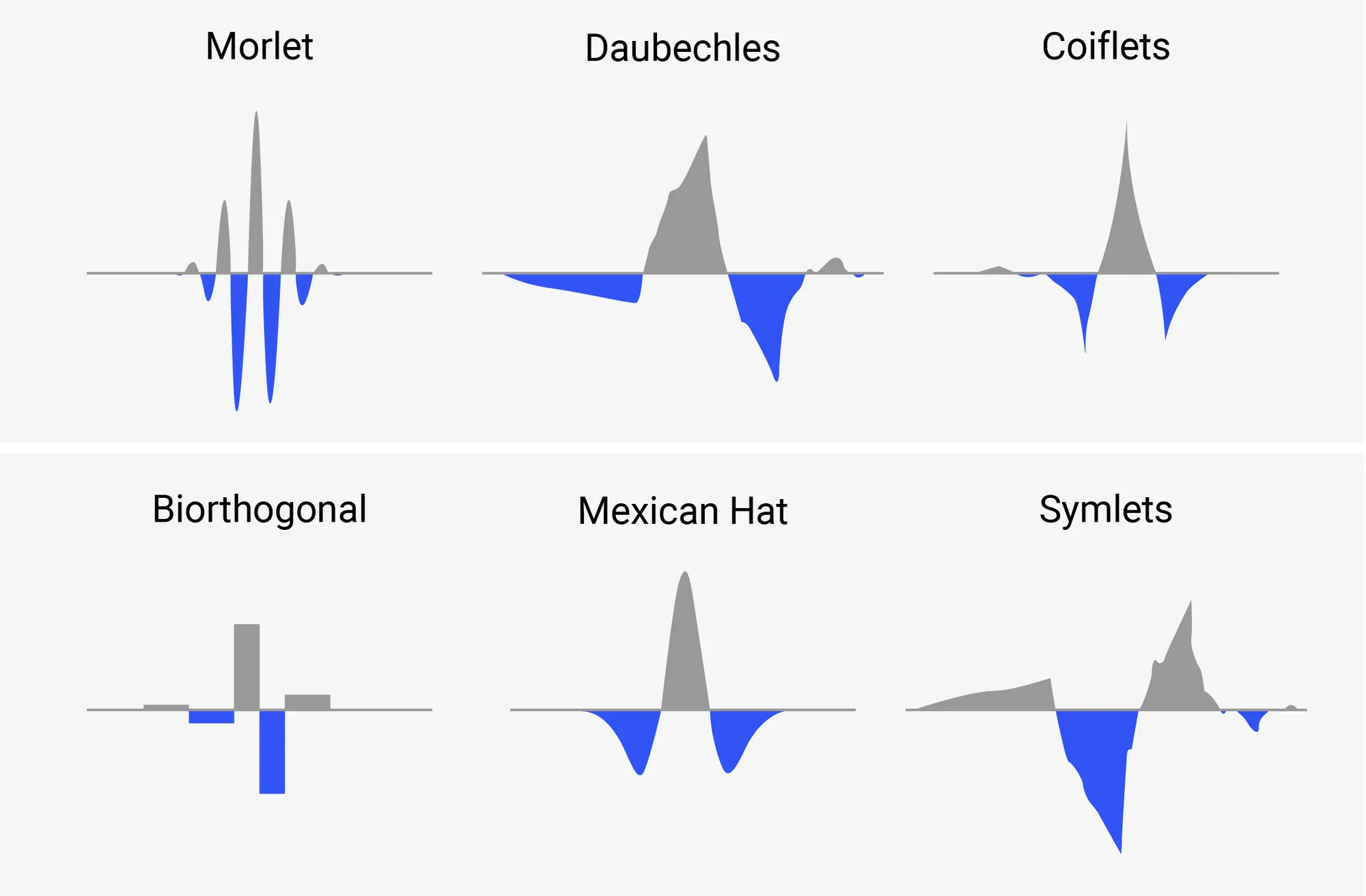
웨이블릿에 대한 정의는 분야마다 조금씩 차이를 보이지만 기본적으로 정해진 시간 안에서 증가와 감소를 반복하며 진동하는, 평균이 0인 진동으로 표현됩니다. 대부분의 웨이블릿 함수는 불규칙적이고 비대칭적이며, 처음 0에서 시작해 진폭이 점점 커지다가 다시 작아지며 0으로 수렴하는 모습을 보입니다. 이러한 특징만 충족시키면 되기 때문에 종류가 무한하며, 대표적으로 Morlet, Coiflet, Symlets, Mexican Hat 등이 있습니다(그림 1).

그림 1. Wavelet의 종류

Scaling and Shifting

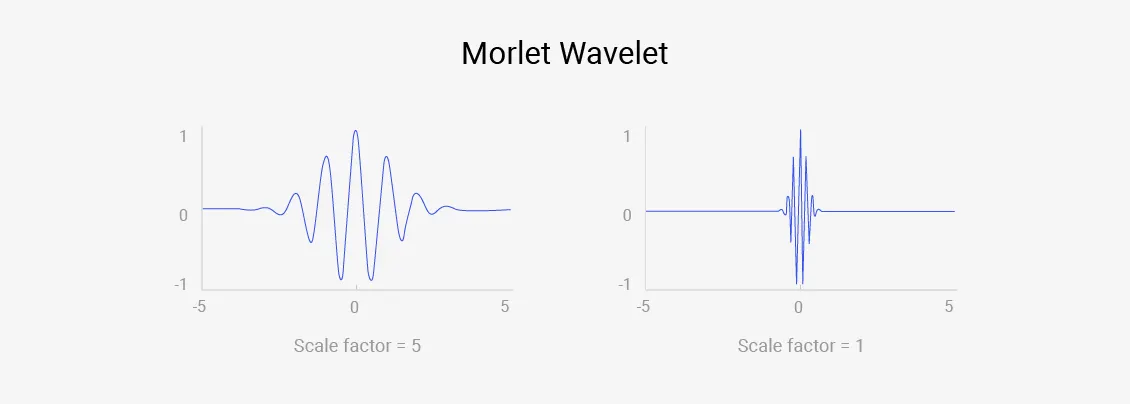
웨이블릿은 기본적으로 파장을 조정할 수 있습니다. 그림 2와 같이 웨이블릿의 길이를 시간축 방향으로 늘리거나 줄이며 조정함으로 저주파수에서 고주파수까지 다양한 대역을 갖는 웨이블릿을 만들어낼 수 있습니다.

그림 2. Scale factor를 조정해 wavelet의 주파수 조정

웨이블릿 변환을 수식으로 표현하면 다음과 같습니다.

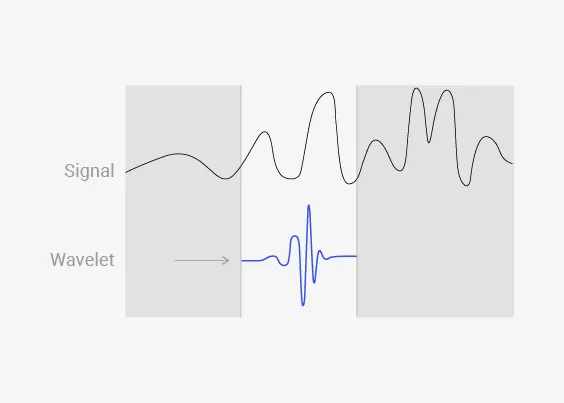
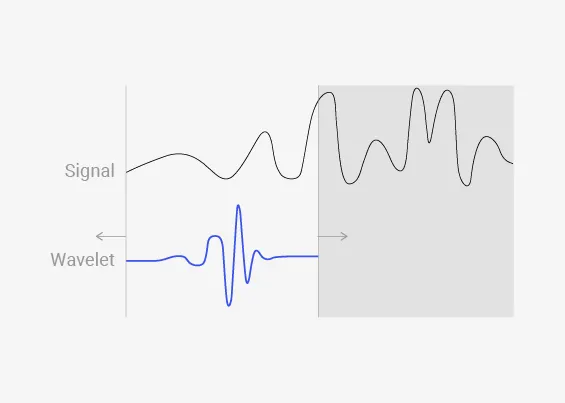
T(a,b)=\frac{1}{\sqrt{a}}\int_{-\infty}^{\infty}x(t)\psi^{*}\frac{t-b}{a}dt

웨이블릿 변환에 사용되는 웨이블릿 함수(mother wavelet)는

\psi

(

{*}

은 복소수 연산을 의미)로 표현되며,

a

와

b

는 각각 웨이블릿의 스케일(scale)과 위치 변화(shifting)를 나타내는 지표입니다. 즉, 웨이블릿 변환이란, 웨이블릿을 시간축 방향으로 이동시켜가며(그림 3) 원본 신호

x(t)

와의 상관계수를 계산하고, 그런 다음 웨이블릿의 스케일을 조정해(그림4) 다시 시간축 방향으로 이동시키며 상관계수를 계산하는 과정을 반복하는 것입니다.

그림 3. Shifting 과정

그림 4. Scailing 과정

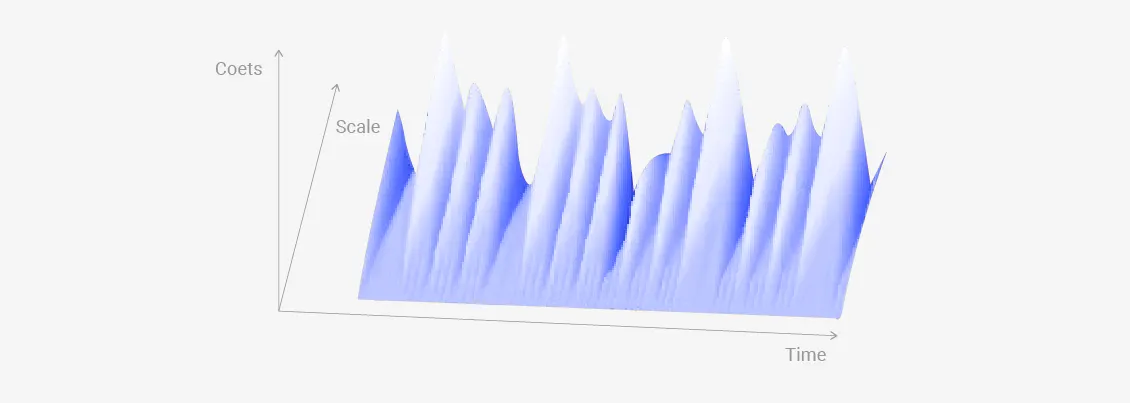
결과적으로 아래 그림5와 같이 x축은 시간, y축은 스케일 지표인 2D 이미지 형태로 결과를 나타낼 수 있으며, 스케일을 웨이블릿의 중심주파수로 변환해 y축을 주파수 값으로 나타낼 수 있습니다.

그림 5. 시계열 데이터의 연속 웨이블릿 변환 결과

Implementation with Python

웨이블릿 변환의 개념은 1900년대부터 등장했으며, 현대에 와서는 다양한 연구를 통해 효율적인 계산 알고리즘들이 여럿 제안되었습니다. 때문에 연속 웨이블릿 변환(Continuous Wavelet Transform, 이하 CWT)은 이미 여러 오픈소스에서 구현된 코드를 확인할 수 있지만, 코드를 확인하면 각각의 계산 방식은 조금씩 상이하다는 것을 알 수 있습니다. 이번 구현에서는 코드가 단순하면서 계산 효율적인 방식으로 CWT 결과를 도출해낼 수 있도록 만들어보겠습니다.

Morlet Wavelet

먼저 웨이블릿으로는 자주 사용되는 Morlet을 사용하겠습니다. 참고 문헌[1]에서는 시간 도메인에서 Morlet wavelet 함수를 다음과 같이 정의하고 있습니다.

\psi(t)=\pi^{-1/4}e^{iw_0t}e^{-t/2}

웨이블릿 변환을 위해서는 웨이블릿의 길이를 조정할 수 있게 하여 다양한 주파수의 웨이블릿을 만들어낼 수 있어야 합니다. 웨이블릿의 길이를 변수로 받아 웨이블릿을 출력해내는 코드는 아래와 같습니다.

import numpy as np
def psi(T, f0=6):
    '''
	  T : parameter for adjusting length of wavelet
	  f0 : parameter for time-frequenct resolution trade off 
    '''
    x = np.linspace(-2 * np.pi, 2 * np.pi, T)
    return (np.pi ** -0.25) * np.exp(1j * f0 * x - x ** 2 / 2)
Python
복사

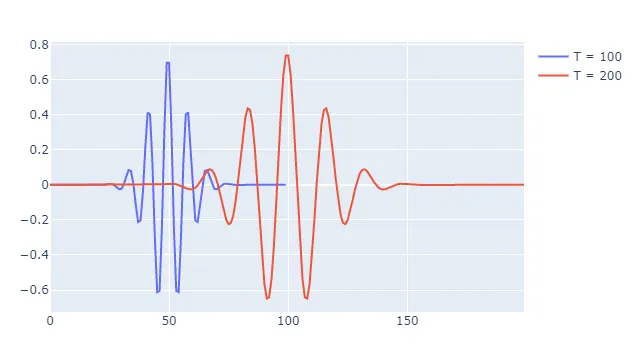
구현된 웨이블릿을 시각화 시켜보면 다음과 같습니다. 1D signal로 표현하기 위해 그래프에서는 실수부만을 사용해 시각화 시킵니다.

그림 6. wavelet 길이 조정 결과

그림과 같이 파라미터 T를 조정해 웨이블릿의 길이를 조정하였습니다. 웨이블릿의 길이가 길수록 저주파수 대역을, 짧을수록 고주파수 대역을 포착해낼 수 있습니다.

Convolution using FFT

앞선 개념 설명 단계에서 웨이블릿 변환의 개념을 정리하면서 웨이블릿 변환은 웨이블릿과 신호 간의 상관계수(correlation coefficient)를 뽑아내는 과정이라 정리했습니다. 상관 계수를 구하기 위해 이번 구현에서는 convolution을 사용합니다. 또한 계산 복잡도를 절감하기 위해 FFT에 기반한 convolution 연산을 사용하겠습니다.

Convolution(합성곱) 연산을 수식적으로 표현하면 다음과 같습니다.

(f*g)(t)=\int_{-\infty}^\infty f(\tau)g(t-\tau)\ d\tau

시간 도메인 상에서 합성곱 연산을 수행하는 방식은 위에서 설명한 웨이블릿 연산의 방법과 마찬가지로 신호

f

에 대해 길이가 더 짧은 신호

g

가

t

축 방향으로 이동하며 벡터간의 곱을 모두 더한 값을 출력하게 됩니다. 그러나 이 방식의 계산 복잡도는

O(n^2)

로, 연산하는 신호가 길어질수록 계산 시간이 기학급수적으로 증가합니다.

시간 도메인에서의 Convolution의 계산 복잡도

Convolution은 연산 과정에서 FFT(Fast Fourier Transform, 고속 푸리에 변환)를 사용해 계산 복잡도를 이보다 단축시킬 수 있습니다. 연산할 두 신호에 대해 zero-padding을 가해 두 신호의 길이를 맞춘 후, FFT를 통해 신호를 주파수 도메인으로 변환합니다. 시간 도메인에서의 convolution 연산은 주파수 도메인에서 곱 연산으로 수행할 수 있기 때문에 두 신호를 곱한 후 결과를 IFFT(Inverse Fourier Transform, 역 고속 푸리에 변환)을 취해 시간 도메인으로 나타냅니다. 이러한 과정이 convolution과 동일함은 참고문헌[2]를 통해 그 증명을 확인하실 수 있습니다. 결과적으로 FFT에 기반한 convolution의 pseudo code로 나타내면 Algorithm1과 같습니다.

Algorithm 1 : Convolution using FFT

계산 과정에서 가장 큰 복잡도를 지닌 FFT와 IFFT 과정의 계산 복잡도에 따라 convolution의 계산 복잡도는

O(nlog_2(n))

으로 정리될 수 있습니다. 이런 계산 복잡도를 감안한 설계는 신호의 길이가 짧을 때는 큰 차이가 없지만, 신호가 길어질수록 계산 시간을 기하급수적으로 절감할 수 있습니다.

이제 위 과정을 python으로 구현하면 다음과 같습니다. FFT와 IFFT 연산은 scipy 라이브러리를 사용했습니다.

from scipy.fft import fft, ifft

def wavelet_convolution(f, T):
    '''
    f : input signal
    T : length of wavelet
    '''
    f_len = np.shape(f)[0]
    f_hat = np.append(f, np.zeros(T))
    h = psi(T)
    h_hat = np.append(h, np.zeros(f_len))
    return ifft(fft(f_hat)*fft(h_hat))[round(T/2) : round(T/2) + f_len]
Python
복사

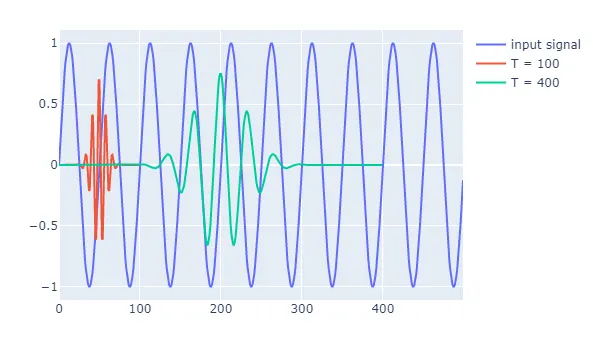
이제 임의의 sin파 신호를 만들어 웨이블릿과 convolution해 결과를 확인해보겠습니다. 웨이블릿의 길이에 따른 convolution의 변화도 확인하기 위해 2개의 웨이블릿을 준비합니다. 첫 번째 웨이블릿의 길이가 100으로 상대적으로 고주파수를, 두 번째 웨이블릿은 길이가 400으로 상대적으로 저주파수를 띕니다. 입력 신호와 첫 번째, 두 번째 웨이블릿을 함께 시각화 시키면 그림7과 같습니다.

그림 7. 다른 길이의 웨이블릿과 입력 신호 비교

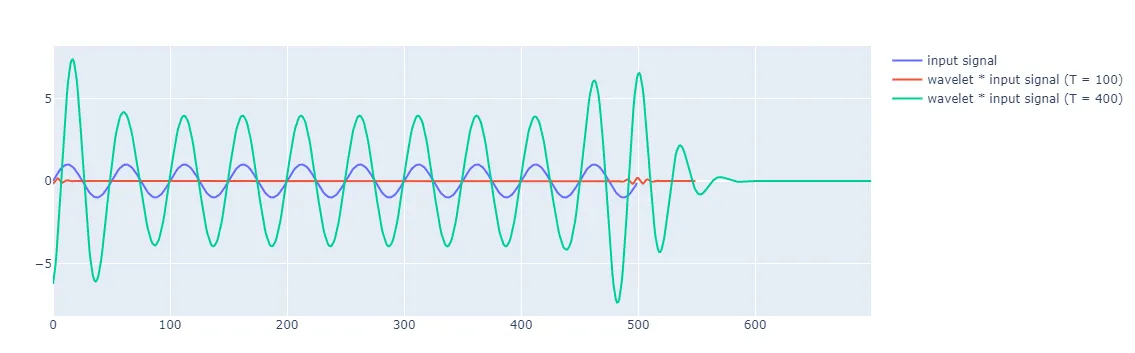
그림에서 보이듯 길이가 400인 웨이블릿은 입력 신호와 거의 비슷한 수준의 주파수를 띄는 것으로 보입니다. 반면 길이가 100인 웨이블릿은 입력신호에 비해 주파수가 높습니다. 이제 convolution 결과를 확인해보면 그림8과 같습니다.

그림 8. 다른 길이의 웨이블릿과 입력신호의 convolution 결과

길이가 100인 웨이블릿은 입력신호와 유사도가 매우 낮기 때문에 convolution 후 값이 매우 낮습니다. 반면 길이가 400인 웨이블릿과의 convolution 결과는 입력신호와 파장이 거의 유사해 매우 높은 값을 보입니다. 즉, 입력신호에는 길이가 100인 웨이블릿의 주파수 성분은 거의 포함되지 않았지만 길이가 400인 웨이블릿의 주파수 성분은 매우 많이 담고 있다고 해석할 수 있습니다.

이렇게 웨이블릿의 파장을 바꿔가며 convolution을 취해 해당 신호에서 어떤 주파수 성분이 얼마나 담겨있는지를 알 수 있습니다.

Pseudo-code and Full-code

앞선 과정을 통해 연산에 필요한 모든 과정을 정리했습니다. 이제 마무리로 CWT를 함수로 구현해보도록 하겠습니다. 먼저 pseudo-code를 작성하면 Algorithm2와 같습니다. scale factor를 파라미터로 받는 웨이블릿에 대해 scale factor를 바꿔가며 원본 신호와 컨볼루션 연산을 반복합니다.

Algorithm 2 : Continuous Wavelet Transform

앞선 과정에서 이미 wavelet의 convolution 함수는 구현을 하였기 때문에 이제 이 함수에 wavelet의 길이만 바꿔가며 입력하면 됩니다. 여러 오픈소스에서는 신호의 길이를 감안해 적절한 scaling의 범위를 추천해주기도 하지만 이번 구현에서는 웨이블릿의 길이를 정해진 최소길이부터 입력신호의 길이까지 10씩 증가시켜가며 변환해보겠습니다. 구현 코드는 다음과 같습니다.

def wavelet_convolution(tup):
    f = tup[0]
    T = tup[1]
    f_len = np.shape(f)[0]
    f_hat = np.append(f, np.zeros(T))
    h = psi(T)
    h_hat = np.append(h, np.zeros(f_len))
    return ifft(fft(f_hat)*fft(h_hat))[round(T/2) : round(T/2) + f_len]

def cwt(f, t0 = 20):
    '''
    f : input signal
    t0 : minimum length of wavelet
    '''
    f_len = np.shape(f)[0]
    result = np.array(list(map(wavelet_convolution, [(f, x) for x in range(t0, f_len, 10)])))
    return result
Python
복사

코드가 매우 간단합니다. 파라미터를 바꿔가며 wavelet_convolution 함수에 편히 입력할 수 있도록 wavelet_convolution 함수에서도 튜플 형태로 파라미터를 입력받게 합니다.

이제 최종적으로 아래 실험을 통해 결과를 확인해보도록 하겠습니다.

Experiment

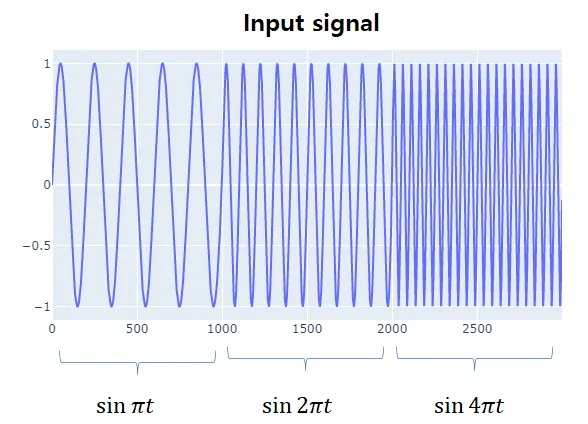
이제 최종적으로 변환할 신호를 준비해 결과를 확인하겠습니다. 준비한 신호는 그림9와 같습니다. 웨이블릿의 특징을 잘 확인하기 위해 시간의 변화에 따라 주파수 특성이 변하는 신호를 준비했습니다.

def input_signal():
    
    x1 = np.linspace(0.0, 10, 1000, endpoint=False)
    x2 = np.linspace(0.0, 10, 1000, endpoint=False)
    x3 = np.linspace(0.0, 10, 1000, endpoint=False)

    y1 = np.sin(1*np.pi*x1)
    y2 = np.append(y1, np.sin(2*np.pi*x2))
    y3 = np.append(y2, np.sin(4*np.pi*x3))

    print(np.shape(y3))
    fig = go.Figure()
    fig.add_trace(go.Scatter(y=y3, mode="lines"))
    fig.show()
    return y3
Python
복사

그림 9. 시간에 따라 주파수 특성이 변하는 입력 신호 구현 결과

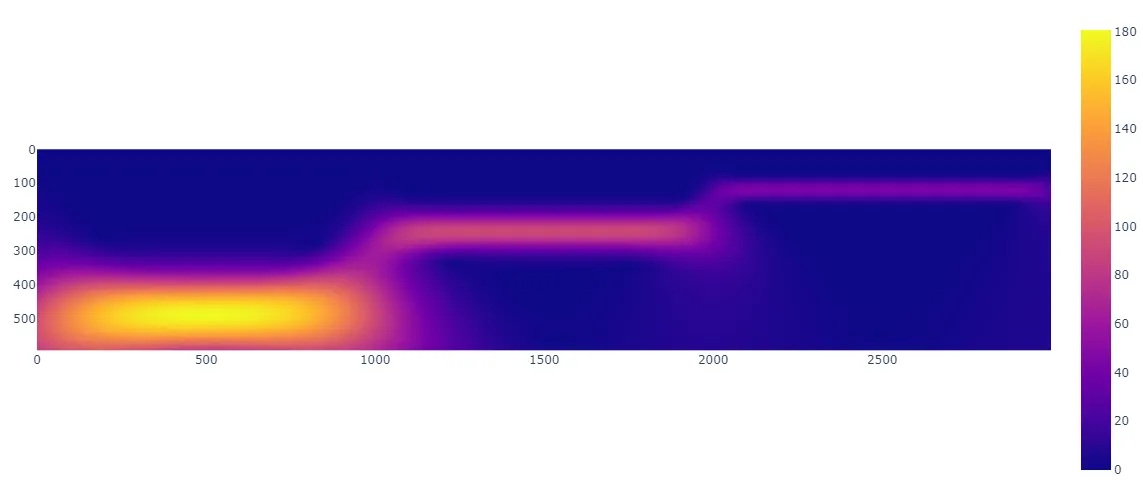
이제 변환할 신호 x에 대한 웨이블릿 변환의 결과를 확인하면 그림10과 같습니다. 복소수를 값으로 갖는 2D 이미지에서 절대값을 취해 그 크기만 남겨 이미지로 시각화 시켰습니다. 이미지의 행은 웨이블릿의 길이, 즉 주파수 성분을 대변하는 값이며, 열은 시간입니다. 첫 행에서부터 마지막 행까지 순차적으로 wavelet의 길이가 길어지기 때문에 상단의 행은 고주파수 성분에, 하단의 행은 저주파수 성분에 반응합니다.

그림 10. CWT 변환 결과

저주파수 성분이 고주파수 성분에 비해 번지듯 여러 행에 걸쳐서 표현된 이유

결과적으로 신호의 좌측에 배치된 저주파수 성분은 저주파수 웨이블릿이 반응했고, 중앙부와 우측에 배치된 고주파수 성분에도 순차적인 고주파수 웨이블릿이 반응하는 그림이 만들어졌습니다.

Conclusion

SW 업계에서는 '바퀴의 재발명'이라는 관용문이 있습니다. 이미 다른 사람들에 의해 만들어진 것을 다시 만드는 작업은 무의미하다는 뜻인데요. 오픈소스 생태계가 기반으로 하는 핵심 가치관이 아닐까 싶습니다.

하지만 연구를 하는 입장에서는 사용하는 코드에 대해 완전히 주도하지 못하고 있다는 불안감을 떨쳐버리기 어렵습니다. 손쉽게 install한 코드가 수학적인 이론을 탄탄하게 구현했는지, 내가 원하는 방향대로 응용해 사용할 수 있는지에 대해 의심하고 검증하는 과정들이 모여 좋은 연구 결과를 도출할 수 있다고 생각합니다. 어느 정도가 적절한 선인지 항상 고민이 필요한 것 같습니다.

이상으로 이번 글을 마치겠습니다. 감사합니다.

[참조]

[1] Torrence, C. and Compo, G. P.. A Practical Guide to Wavelet Analysis. Bulletin of the American Meteorological Society, American Meteorological Society, 1998, 79

[2] Yi H. Xin S-Y. and Yin J-F. A Class of Algorithms for Continuous Wavelet Transform Based on the Circulant Matrix, Algorithms, 2018, 3

이 글을 쓴 사람

주 요 한 | 감마 팀

무언가를 만들고 사람들과 함께하는걸 좋아합니다.

원프레딕트에서 산업용 로봇 진단 솔루션을 개발하고 있습니다. 주말엔 등산도 하고 마라톤도 나가고 회사에서 몰래 빔프로젝터로 영화도 보고.. 아 나는 왜 글까지 잘써서 기술블로그를 담당하고 있을까

원프레딕트 홈페이지 https://onepredict.ai/

원프레딕트 블로그 https://blog.onepredict.ai/

원프레딕트 기술 블로그 https://tech.onepredict.ai