Intro.
특정 데이터에 대한 예측 모델을 만들기 위해서는 데이터에 존재하는 중요한 정보들을 추출할 필요가 있습니다. 이를 위해 우리가 가진 지식을 이용해 데이터에 다양한 가공 과정을 거치는데, 이를 데이터 전처리라고 합니다.
데이터 특성에 따라 적합한 전처리 과정은 서로 다를 수 있습니다. 가령 진동 데이터의 경우 주파수 분석을 위해 Fast Fourier Transformation (FFT), Short Time Fourier Transformation (STFT)를 수행하는 경우가 많고, 이미지 데이터의 경우 주요한 부분을 추출하기 위해 blob detection, ridge detection과 같은 전처리를 수행하는 경우가 많습니다.
저희가 진단하는 터빈의 경우 대부분 주기적으로(e.g. 10초, 1분 마다) 값이 추출되는 시계열 데이터가 분석 대상이 됩니다. 시계열 데이터에도 다양한 전처리 방법들이 있지만, 데이터들 간의 연관성이 높은 터빈 데이터에서는 시간에 따른 상관관계의 변화를 파악하는 것이 중요합니다. 갑작스러운 상관관계의 변화가 고장에 대한 신호가 되기도 하고, 상관관계를 이용하여 진단 및 예측 모델을 개선할 수도 있기 때문입니다.
따라서 이러한 시계열 상관관계 (time-series correlation)의 중요성 및 활용 방안, 분석 알고리즘에 대해 작성하였습니다.
Time-series Correlation
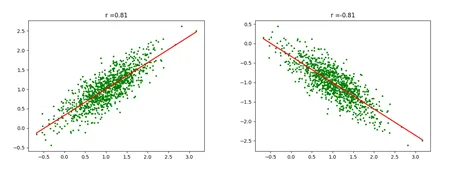
Correlation이란 2개의 변수가 가지는 선형 상관관계를 의미합니다. Collinearity는 Regression Model을 생성할 때 독립변수 중 2개 이상이 강한 선형 상관관계를 가지는 상황을 뜻합니다. 예를 들어, Figure 1과 같이 두 변수가 함께 상승하는 경향을 갖거나, 반대의 증감 경향을 보이는 경우가 발생합니다.
Figure 1. 강한 양의 상관관계(0.81)와 음의 상관관계(-0.81)를 가지는 데이터
Multicollinearity는 collinearity의 특별한 케이스인데, 3개 이상의 독립변수 사이에서 강한 선형 상관관계가 나타나는 경우입니다. 이러한 multicollinearity는 예측 모델에서의 파라미터 예측이 불안정해지게 만듭니다. 몇 개의 특정 파라미터가 매우 커져 조그만 데이터의 변화에도 결과값이 크게 달라질 수 있으며, 학습 때마다 모델이 매번 다른 결과를 도출할 수도 있게 됩니다.
위와 같은 불안정성을 피하기 위해 변수들간 연관성을 찾아 미리 알고 모델을 구성하는 것이 중요합니다. 따라서, Time-series 데이터간 correlation을 찾는 몇 가지 방법에 대해 알아보겠습니다.
1. Pearson Correlation Coefficient(피어슨 상관 계수)
Pearson 상관 계수는 두 변수간의 선형 상관관계를 계량화한 수치입니다. Pearson 상관 계수는 +1과 -1 사이의 값을 가지며, +1은 완벽한 양의 선형 상관 관계, 0은 선형 상관 관계없음, -1은 완벽한 음의 선형 상관 관계를 의미합니다.
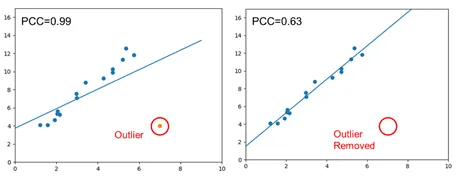
전체 구간에 대해 두 변수가 선형 연관성이 어떠한지 나타낸 결과이므로 두 데이터의 인과관계에 대한 정보는 없습니다. 다시 말해, 한 변수가 증가할 때 다른 변수가 증가 또는 감소하는지에 대한 정보는 얻을 수 있어도, 두 변수 중 어느 변수가 다른 변수에 영향을 주는지에 대한 정보는 얻을 수 없습니다. 또한 Pearson Correlation은 데이터가 등분산성을 가진다고 가정하므로 변수 데이터가 정규 분포를 가지지 않거나 outlier가 발생할 경우 잘못된 분석 결과가 도출될 수 있습니다. 가령 Figure 2와 같이, Pearson 상관 관계가 0.99인 데이터셋에 outlier가 하나만 추가되더라도 Pearson 상관 계수가 0.63으로 떨어지면서 데이터에 대한 부정확한 분석 결과가 도출된다는 것을 볼 수 있습니다.
Figure 2. Outlier 유무에 따른 PCC의 변화
2. Kendall Tau Rank Correlation Coefficient (켄달 상관 계수)
Kendall Tau Correlation Coefficient은 순위 상관 계수(Rank Correlation Coefficient)의 한 종류이며 두 변수들 간의 순위를 비교하여 연관성을 계산합니다. Pearson과 같이 두 데이터의 연관성을 +1과 -1 사이의 값으로 나타내고, 전체 구간에 대한 결과입니다.
두 변수간 데이터 그 자체가 아닌 순위를 비교하는 것이기에, 변수 데이터가 정규 분포를 가지지 않으면 잘못된 결과를 얻을 수 있는 Pearson 상관 계수의 단점이 보완됩니다.
3. Time Lagged Cross Correlation (TLCC)
TLCC는 하나의 time-series를 조금씩 shifting 시키면서 데이터 전체 범위에 대하여 Pearson 상관 계수를 계산하여 나타냅니다. TLCC는 Pearson, Kendall Correlation과는 다르게 두 데이터 사이에서의 인과관계를 파악할 수 있습니다.
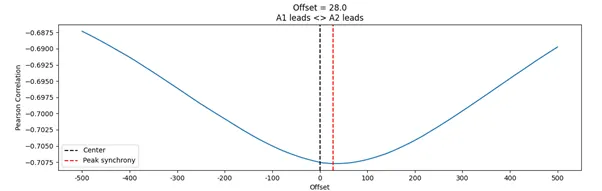
이러한 인과관계의 대표적인 것으로는 leader-follower relationship이 있습니다. 이에 대한 예시로 Figure 3에서 터빈 데이터 A1과 A2의 TLCC 결과를 나타냈습니다. A2의 shift범위를 -500~+500까지의 값을 계산하여 shift에 따라 상관 계수 값의 변화를 관찰하였습니다.
Figure 3. Shift가 -500~500일 때의 TLCC
결과를 보면 A2가 앞으로 28만큼 shift 되었을 때 상관관계의 절댓값이 가장 높게 측정되었습니다. Offset이 양의 값이므로 A2가 이 상관관계를 주도한다는 것을 알 수 있습니다. TLCC는 전체 구간에 대한 결과이므로, 추가적으로 시간에 따라 상세하게 분석을 하고자 한다면 Windowed Time Lagged Cross Correlation (WTLCC)을 사용하면 됩니다. 데이터를 여러 개의 window로 나누고 위와 같은 TLCC분석을 각 window마다 하는 것이 WTLCC입니다.
4. Dynamic Time Warping (DTW)
DTW는 Figure 4와 같이, 두 time-series 데이터 간의 최소거리를 가지는 직선 경로를 찾는 방식입니다. 데이터 각 시간 지점에서 길이를 구하는 것이 Euclidean 방식이고, 데이터 각 지점에서 시간지점과 상관없이 최단 직선 경로를 찾는 것이 DTW입니다. Signal의 길이가 서로 다르더라도 DTW를 적용할 수 있다는 장점이 있습니다. 이러한 장점이 있어 Speech analysis에 사용하기 위해 처음 개발되었습니다.
Figure 4. Euclidean과 DTW의 차이
Conclusion
시계열 데이터의 상관 관계를 파악하기 위해 사용될 수 있는 분석 방법에 대해 알아보았습니다.
정해진 구간 안에서 두 시계열 데이터의 상관 관계를 수치로 나태내는 방식으로 피어슨 상관 계수와 켄달 상관계수가 있었으며, 두 시계열 데이터의 인과관계를 파악하기 위한 방식으로는 TLCC가 있었습니다. 마지막으로 다른 길이를 가지는 시계열의 유사성을 판단하기 위한 방식으로는 DTW를 소개하였습니다.
시계열 데이터 중에서도 터빈 데이터는 데이터들 간의 연관성이 높기 때문에 상관 관계 분석이 중요합니다. 시간에 따라 구간을 나누어 1) 데이터의 상관 관계에 변화가 발생하는지와 2) 인과관계가 어떻게 되는지를 분석한다면, 특정 현상의 인과관계를 설명할 수 있게 됩니다.
이를 활용한다면 터빈 시스템의 진단 및 예측 모델의 정확도 향상에 기여할 수 있습니다.
이 글을 쓴 사람
이 동 준 | Product 2팀
원프레딕트 Product 2팀 Data Scientist입니다.
회사 출근도 처음이고 모르는 것도 많아 매일매일이 새롭습니다. 스키, 테니스, 축구처럼 운동하는 것을 좋아합니다. 새로운 도전도 좋아해서 원프레딕트에서도 많이 성장하고 싶습니다.